题目内容
13.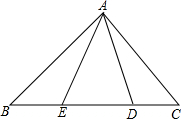 如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°.设BE=a,DC=b,那么AB=$\frac{\sqrt{2}}{2}$(a+b+$\sqrt{{a}^{2}+{b}^{2}}$)(用含a、b的式子表示AB).
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°.设BE=a,DC=b,那么AB=$\frac{\sqrt{2}}{2}$(a+b+$\sqrt{{a}^{2}+{b}^{2}}$)(用含a、b的式子表示AB).
分析 将△ADC绕点A顺时针旋转90°后,得到△AFB,只要证明△FAE≌△DAE,推出EF=ED,∠ABF=∠C=45°,由∠EBF=∠ABF+∠ABE=90°,推出ED=EF=$\sqrt{{a}^{2}+{b}^{2}}$,可得BC=a+b+$\sqrt{{a}^{2}+{b}^{2}}$,根据AB=BC•cos45°即可解决问题.
解答 解:将△ADC绕点A顺时针旋转90°后,得到△AFB.
证明:∵△DAC≌△FAB,
∴AD=AF,∠DAC=∠FAB,
∴∠FAD=90°,
∵∠DAE=45°,
∴∠DAC+∠BAE=∠FAB+∠BAE=∠FAE=45°,
在△FAE和△DAE中,
$\left\{\begin{array}{l}{DA=FA}\\{∠DAE=∠FAE}\\{AE=AE}\end{array}\right.$,
∴△FAE≌△DAE,
∴EF=ED,∠ABF=∠C=45°,
∵∠EBF=∠ABF+∠ABE=90°,
∴ED=EF=$\sqrt{{a}^{2}+{b}^{2}}$,
∴BC=a+b+$\sqrt{{a}^{2}+{b}^{2}}$,
∴AB=BC•cos45°=$\frac{\sqrt{2}}{2}$(a+b+$\sqrt{{a}^{2}+{b}^{2}}$).
故答案为$\frac{\sqrt{2}}{2}$(a+b+$\sqrt{{a}^{2}+{b}^{2}}$).
点评 本题考查旋转变换、等腰直角三角形的性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
7.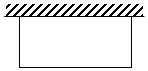 用28米长的铁丝围成一个一边靠墙的长方形.
用28米长的铁丝围成一个一边靠墙的长方形.
(1)当垂直于墙的一边比另一边少7米时,求长方形的面积.
(2)按表中列出的数据要求,填写表格.
观察表格,你感到长方形的面积会不会有最大的情况?如果会,可能是多少?
 用28米长的铁丝围成一个一边靠墙的长方形.
用28米长的铁丝围成一个一边靠墙的长方形.(1)当垂直于墙的一边比另一边少7米时,求长方形的面积.
(2)按表中列出的数据要求,填写表格.
观察表格,你感到长方形的面积会不会有最大的情况?如果会,可能是多少?
| 垂直于墙的一边比另一边少(m) | 1 | 4 | 7 | 10 | 13 |
| 长方形的面积 | 90 | 96 | 98 | 96 | 90 |
2. 如图,AB∥EF∥CD,EG∥BD,且BD平分∠ABC,则图中与∠1相等的角(∠1除外)共有( )
如图,AB∥EF∥CD,EG∥BD,且BD平分∠ABC,则图中与∠1相等的角(∠1除外)共有( )
 如图,AB∥EF∥CD,EG∥BD,且BD平分∠ABC,则图中与∠1相等的角(∠1除外)共有( )
如图,AB∥EF∥CD,EG∥BD,且BD平分∠ABC,则图中与∠1相等的角(∠1除外)共有( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
 如图所示,在△ABC中,AD为BC边上的中线,且AD平分∠BAC,求证:AB=AC.
如图所示,在△ABC中,AD为BC边上的中线,且AD平分∠BAC,求证:AB=AC.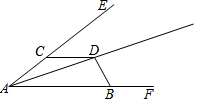 如图,D是∠EAF平分线上一点,点C、B分别在射线AE、AF上且CD=BD(AB>AC).
如图,D是∠EAF平分线上一点,点C、B分别在射线AE、AF上且CD=BD(AB>AC).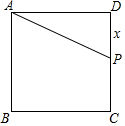 如图,正方形ABCD的边长为2,P为DC上的点(不与C,D点重合).设线段DP的长为x,求梯形ABCP的面积y关于x的函数关系式,并写出自变量x的取值范围.
如图,正方形ABCD的边长为2,P为DC上的点(不与C,D点重合).设线段DP的长为x,求梯形ABCP的面积y关于x的函数关系式,并写出自变量x的取值范围.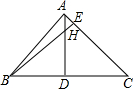 如图,AD、BE是△ABC的两条高,AD=BD,H是高AD与BE的交点,试问:BH与AC的长度相等吗?说明你的理由.
如图,AD、BE是△ABC的两条高,AD=BD,H是高AD与BE的交点,试问:BH与AC的长度相等吗?说明你的理由. 如图,已知AC∥DE,∠A=∠E,BD=CF,求证:AB∥EF.
如图,已知AC∥DE,∠A=∠E,BD=CF,求证:AB∥EF.