题目内容
16. 如图所示,AE是△ABD的中线,CE是△BCD的高,E在AC上,若S△ABE=4,AE:EC=3:2,求四边形ABCD的面积.
如图所示,AE是△ABD的中线,CE是△BCD的高,E在AC上,若S△ABE=4,AE:EC=3:2,求四边形ABCD的面积.
分析 根据题意设AE=3x,EC=2x,由S△ABE=4,得出BD=$\frac{16}{3x}$,然后根据S四边形ABCD=S△ABD+S△BCD求得即可.
解答 解:∵AE:EC=3:2,
∴设AE=3x,EC=2x,
∵S△ABE=4,
∴$\frac{1}{2}$BE•AE=4,即$\frac{1}{2}$BE•3x=4,
∴BE=$\frac{8}{3x}$,
∵AE是△ABD的中线,
∴BD=$\frac{16}{3x}$,
∵CE是△BCD的高,E在AC上,
∴AC⊥BD,
∴S四边形ABCD=S△ABD+S△BCD=$\frac{1}{2}$BD•3x+$\frac{1}{2}$BD•2x=8+$\frac{16}{3}$=$\frac{40}{3}$.
点评 本题考查了三角形面积公式的应用,正确表示出BD的长是解题的关键.

练习册系列答案
相关题目
1.下列命题中是真命题的是( )
| A. | 阴天会下雨是必然事件 | |
| B. | 若关于x的一元二次方程kx2-2x-1=0有实数根,则k≥-1 | |
| C. | 在平面直角坐标系中,如果位似是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k | |
| D. | 多边形的外角和等于360° |
6.若m与-3互为倒数,则m等于( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
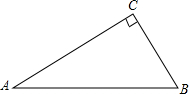 如图,△ABC中,∠ACB=90°,BC=$\sqrt{5}$,AC=2$\sqrt{5}$,
如图,△ABC中,∠ACB=90°,BC=$\sqrt{5}$,AC=2$\sqrt{5}$,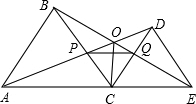 如图,C为线段AE上一动点(不与点A,E重合),在AE在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤OC平分∠AOE.一定成立的结论有①②③⑤.
如图,C为线段AE上一动点(不与点A,E重合),在AE在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤OC平分∠AOE.一定成立的结论有①②③⑤.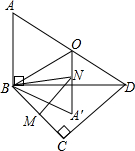 如图,一副三角板△BCD拼在一起,O为AD的中点,AB=4,将△ABO沿BO对折到△A′BO处,M为边BC上一动点,N为直线A′O一动点,则NB+NM的最小值为2$\sqrt{6}$.
如图,一副三角板△BCD拼在一起,O为AD的中点,AB=4,将△ABO沿BO对折到△A′BO处,M为边BC上一动点,N为直线A′O一动点,则NB+NM的最小值为2$\sqrt{6}$.