题目内容
7.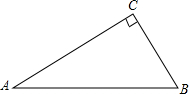 如图,△ABC中,∠ACB=90°,BC=$\sqrt{5}$,AC=2$\sqrt{5}$,
如图,△ABC中,∠ACB=90°,BC=$\sqrt{5}$,AC=2$\sqrt{5}$,(1)若⊙C切AB于D,求⊙C半径及切线AD的长;
(2)直接写出⊙C与线段AB有两个公共点时半径r的取值范围.
分析 (1)根据已知和勾股定理求出AB的长,根据面积公式求出⊙C的半径,根据勾股定理求出AD的长;
(2)观察图形可以得到⊙C与线段AB有两个公共点时半径r的取值范围.
解答 解:(1)作CD⊥AB于D,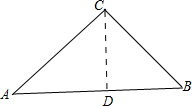
∠ACB=90°,BC=$\sqrt{5}$,AC=2$\sqrt{5}$,
由勾股定理得:AB=5,
$\frac{1}{2}$×AC×BC=$\frac{1}{2}$×AB×CD,
CD=2,
在直角三角形ADC中,AD2=AC2-CD2,
AD=4,
(2)∵CD=2,BC=$\sqrt{5}$,
∴⊙C与线段AB有两个公共点时,2<r≤$\sqrt{5}$.
点评 本题考查的是直线与圆的位置关系,正确通过圆心到直线的距离与圆的半径的关系判断直线与圆的位置关系是解题的关键.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
14.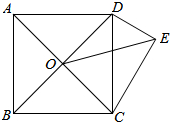 如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=$\frac{\sqrt{6}+\sqrt{2}}{2}$,则正方形的面积为( )
如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=$\frac{\sqrt{6}+\sqrt{2}}{2}$,则正方形的面积为( )
 如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=$\frac{\sqrt{6}+\sqrt{2}}{2}$,则正方形的面积为( )
如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=$\frac{\sqrt{6}+\sqrt{2}}{2}$,则正方形的面积为( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
15.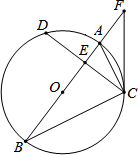 如图,在⊙O中,直径AB平分弦CD,AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.
如图,在⊙O中,直径AB平分弦CD,AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.
(1)求证:CF是⊙O的切线.
(2)若AC=4,CE=2AE,求⊙O的半径.
 如图,在⊙O中,直径AB平分弦CD,AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.
如图,在⊙O中,直径AB平分弦CD,AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.(1)求证:CF是⊙O的切线.
(2)若AC=4,CE=2AE,求⊙O的半径.
2. 如图:△ABC中,DE∥BC,AD=5,BD=10,AE=3.则AC的值为( )
如图:△ABC中,DE∥BC,AD=5,BD=10,AE=3.则AC的值为( )
 如图:△ABC中,DE∥BC,AD=5,BD=10,AE=3.则AC的值为( )
如图:△ABC中,DE∥BC,AD=5,BD=10,AE=3.则AC的值为( )| A. | 9 | B. | 6 | C. | 3 | D. | 4 |
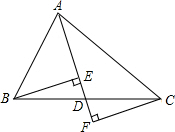 如图,在△ABC中,点D是BC边的中点,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:DE=DF.
如图,在△ABC中,点D是BC边的中点,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:DE=DF.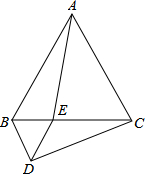 如图所示,△ABC和△BDE都是等边三角形,AE与CD相等吗?说明理由.
如图所示,△ABC和△BDE都是等边三角形,AE与CD相等吗?说明理由. 如图所示,AE是△ABD的中线,CE是△BCD的高,E在AC上,若S△ABE=4,AE:EC=3:2,求四边形ABCD的面积.
如图所示,AE是△ABD的中线,CE是△BCD的高,E在AC上,若S△ABE=4,AE:EC=3:2,求四边形ABCD的面积.