题目内容
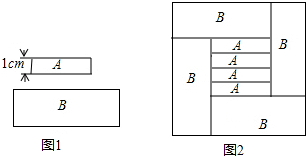 用A、B两种规格的长方形纸板(如图1)无重合无缝隙的拼接可得如图2所示的周长为32cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积是( )
用A、B两种规格的长方形纸板(如图1)无重合无缝隙的拼接可得如图2所示的周长为32cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积是( )| A、10cm2 |
| B、12cm2 |
| C、14cm2 |
| D、16cm2 |
考点:一元一次方程的应用
专题:几何图形问题
分析:可设A长方形的长是xcm,则B长方形的宽是(4-
x)cm,B长方形的长是(8-
x)cm,根据大正方形周长为32cm,列出方程求解即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:设A长方形的长是xcm,则B长方形的宽是(4-
x)cm,B长方形的长是(8-
x)cm,依题意有
4[(4-
x)+(8-
x)]=32,
解得x=4,
(4-
x)(8-
x)
=(4-2)×(8-2)
=2×6
=12.
故B种长方形的面积是12cm2.
故选:B.
| 1 |
| 2 |
| 1 |
| 2 |
4[(4-
| 1 |
| 2 |
| 1 |
| 2 |
解得x=4,
(4-
| 1 |
| 2 |
| 1 |
| 2 |
=(4-2)×(8-2)
=2×6
=12.
故B种长方形的面积是12cm2.
故选:B.
点评:考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
如图所示,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②∠A=∠D;∠B=∠E,∠C=∠F;③AB=DE,BC=EF,∠B=∠E;④AB=DE,∠C=∠F,AC=DF.其中能使△ABC≌△DEF的条件的组数共有( )
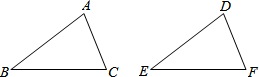

| A、1组 | B、2组 | C、3组 | D、4组 |
 如图,在平面直角坐标系中,已知点A(0,4)、B(-4,0),BE⊥AC于E交y轴于点M(0,a),且∠BMA=105°.下列四个结论:①AE=
如图,在平面直角坐标系中,已知点A(0,4)、B(-4,0),BE⊥AC于E交y轴于点M(0,a),且∠BMA=105°.下列四个结论:①AE=| 1 |
| 2 |
| A、只有①④ | B、只有①③④ |
| C、只有②③ | D、①②③④ |
已知二次函数y=kx2-2x-1(k≠0)的图象与x轴有两个交点,则k的取值范围是( )
| A、k>-1且k≠0 |
| B、k>-1 |
| C、k<1且k≠0 |
| D、k<1 |
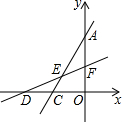 如图,A(0,4),C(-2,0),D(-4,0),过D点的直线交AC于E,交y轴于F,若S△DCE=S△AEF,求E点的坐标.
如图,A(0,4),C(-2,0),D(-4,0),过D点的直线交AC于E,交y轴于F,若S△DCE=S△AEF,求E点的坐标.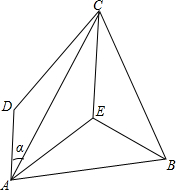 如图,在四边形ABCD中,BA=BC,AC是∠DAE的平分线,AD∥EC,∠AEB=120°.求∠DAC的度数α的值.
如图,在四边形ABCD中,BA=BC,AC是∠DAE的平分线,AD∥EC,∠AEB=120°.求∠DAC的度数α的值.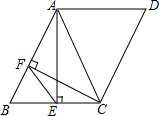 已知如图,在?ABCD中,∠D=60°,AE⊥BC,CF⊥AB,垂足分别为E,F.求证:AC=2EF.
已知如图,在?ABCD中,∠D=60°,AE⊥BC,CF⊥AB,垂足分别为E,F.求证:AC=2EF.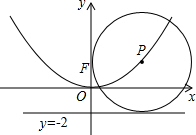 如图,在平面直角坐标系xOy中,若动点P在抛物线y=ax2上,⊙P恒过点F(0,2),且与直线y=-2始终保持相切,则a=
如图,在平面直角坐标系xOy中,若动点P在抛物线y=ax2上,⊙P恒过点F(0,2),且与直线y=-2始终保持相切,则a=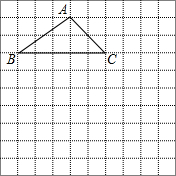 如图所示,在10×10正方形网格中,△ABC的三个顶点都在格点上,请按下列要求画图并回答问题:
如图所示,在10×10正方形网格中,△ABC的三个顶点都在格点上,请按下列要求画图并回答问题: