题目内容
 如图,在平面直角坐标系中,已知点A(0,4)、B(-4,0),BE⊥AC于E交y轴于点M(0,a),且∠BMA=105°.下列四个结论:①AE=
如图,在平面直角坐标系中,已知点A(0,4)、B(-4,0),BE⊥AC于E交y轴于点M(0,a),且∠BMA=105°.下列四个结论:①AE=| 1 |
| 2 |
| A、只有①④ | B、只有①③④ |
| C、只有②③ | D、①②③④ |
考点:全等三角形的判定与性质,坐标与图形性质
专题:
分析:先求出∠ABM=30°,即可得出结论①正确;通过证明△AOC≌△BOM,得出②错误;延长ME至F,使EF=ME,连接AF、CF,证明AB=AF,得出③正确;在AE上截取EG=CE,连接GM、GF,得出四边形MCFG是菱形,证出④正确.
解答:
解:∵A(0,4)、B(-4,0),
∴△OAB时等腰直角三角形,
∴∠OAB=∠OBA=45°,
∵∠BMA=105°,
∴∠ABM=180°-105°-45°=30°,
∵BE⊥AC,∴AE=
AB,
∴①正确;
∵∠BAE=90°-∠ABE=60°,
∴∠OAC=60°-45°=15°,
∵∠OBM=45°-30°=15°,
∴∠OAC=∠OBM,
在△AOC和△BOM中,
,
∴△AOC≌△BOM(ASA),
∴OC=OM=a,
∴C(a,0),
∴②错误;
延长ME至F,使EF=ME,连接AF、CF,如图所示: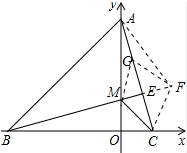
∴AF=AM,
∴CF=CM,
∴∠FAE=∠OAC=15°,
∴∠BAF=45°+15°+15°=75°,∠AFB=75°,
∴AB=BF,
∵OC=OM,
∴∠OMC=45,
∴∠CMF=60°,
∴△CMF是等边三角形,
∴CM=MF,
∴AB=BM+MF=BM+CM,
∴③正确;
在AE上截取EG=CE,连接GM、GF,如图所示:
则四边形MCFG是菱形,
∴∠MGF=60°,
∴∠MGE=30°,
∴∠AMG=30°-15°=15°,
∴GM=AG,
∴CE+CM=GE+AG=AE,
∴④正确;
故选:B.
∴△OAB时等腰直角三角形,
∴∠OAB=∠OBA=45°,
∵∠BMA=105°,
∴∠ABM=180°-105°-45°=30°,
∵BE⊥AC,∴AE=
| 1 |
| 2 |
∴①正确;
∵∠BAE=90°-∠ABE=60°,
∴∠OAC=60°-45°=15°,
∵∠OBM=45°-30°=15°,
∴∠OAC=∠OBM,
在△AOC和△BOM中,
|
∴△AOC≌△BOM(ASA),
∴OC=OM=a,
∴C(a,0),
∴②错误;
延长ME至F,使EF=ME,连接AF、CF,如图所示:

∴AF=AM,
∴CF=CM,
∴∠FAE=∠OAC=15°,
∴∠BAF=45°+15°+15°=75°,∠AFB=75°,
∴AB=BF,
∵OC=OM,
∴∠OMC=45,
∴∠CMF=60°,
∴△CMF是等边三角形,
∴CM=MF,
∴AB=BM+MF=BM+CM,
∴③正确;
在AE上截取EG=CE,连接GM、GF,如图所示:
则四边形MCFG是菱形,
∴∠MGF=60°,
∴∠MGE=30°,
∴∠AMG=30°-15°=15°,
∴GM=AG,
∴CE+CM=GE+AG=AE,
∴④正确;
故选:B.
点评:本题考查了全等三角形的性质和判定以及图形与坐标性质、含30°角的直角三角形的性质;证明三角形全等是解决②的关键;特别是通过作辅助线解决问题③④是常用的方法.

练习册系列答案
相关题目
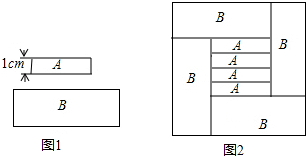 用A、B两种规格的长方形纸板(如图1)无重合无缝隙的拼接可得如图2所示的周长为32cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积是( )
用A、B两种规格的长方形纸板(如图1)无重合无缝隙的拼接可得如图2所示的周长为32cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积是( )| A、10cm2 |
| B、12cm2 |
| C、14cm2 |
| D、16cm2 |
如图,在数轴上有六个点,且AB=BC=CD=DE=EF,则与点C所表示的数最接近的整数是( )

| A、2 | B、1 | C、0 | D、-1 |
 如图,CD∥AB,∠ABF=
如图,CD∥AB,∠ABF= 如图,在四边形ABCD中,∠1=∠2,∠3=∠4,∠B=∠D,AF=CE,AB∥CD.
如图,在四边形ABCD中,∠1=∠2,∠3=∠4,∠B=∠D,AF=CE,AB∥CD.
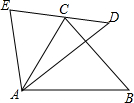 如图,E、C、D三点在一条直线上,AE=AC,AD=AB,∠EAC=∠DAB.求证:△EAD≌△CAB.
如图,E、C、D三点在一条直线上,AE=AC,AD=AB,∠EAC=∠DAB.求证:△EAD≌△CAB. 如图,AB是⊙O的直径,CD是弦,且AB⊥CD,若∠BOC=50°,则∠A=
如图,AB是⊙O的直径,CD是弦,且AB⊥CD,若∠BOC=50°,则∠A=