题目内容
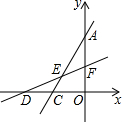 如图,A(0,4),C(-2,0),D(-4,0),过D点的直线交AC于E,交y轴于F,若S△DCE=S△AEF,求E点的坐标.
如图,A(0,4),C(-2,0),D(-4,0),过D点的直线交AC于E,交y轴于F,若S△DCE=S△AEF,求E点的坐标.考点:两条直线相交或平行问题,一次函数图象上点的坐标特征
专题:计算题
分析:利用S△DCE=S△AEF可得S△DOF=S△ACO,再利用三角形面积公式可求出OF=2,则OF(0,2),接着利用待定系数法分别求出直线AC的解析式为y=2x+4,直线DF的解析式为y=
x+2,然后通过解方程组
可得点E的坐标.
| 1 |
| 2 |
|
解答:
解:∵S△DCE=S△AEF,
∴S△DOF=S△ACO,
∴S△DOF=
OF•4=
•4•2,
∴OF=2,
∴F(0,2),
设直线AC解析式为y=kx+b,
把A(0,4)、C(-2,0)分别代入得
,解得
,
∴直线AC的解析式为y=2x+4,
设直线DF的解析式为y=kx+b,
把F(0,2)、D(-4,0)分别代入得
,解得
,
∴直线DF的解析式为y=
x+2,
解方程组
得
,
∴点E的坐标为(-
,-
).
∴S△DOF=S△ACO,
∴S△DOF=
| 1 |
| 2 |
| 1 |
| 2 |
∴OF=2,
∴F(0,2),
设直线AC解析式为y=kx+b,
把A(0,4)、C(-2,0)分别代入得
|
|
∴直线AC的解析式为y=2x+4,
设直线DF的解析式为y=kx+b,
把F(0,2)、D(-4,0)分别代入得
|
|
∴直线DF的解析式为y=
| 1 |
| 2 |
解方程组
|
|
∴点E的坐标为(-
| 4 |
| 3 |
| 4 |
| 3 |
点评:本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;也考查了待定系数法求一次函数解析式.

练习册系列答案
相关题目
 如图,CD是△ABC的角平分线,DE∥BC.若∠A=60°,∠B=80°,则∠CDE的度数是( )
如图,CD是△ABC的角平分线,DE∥BC.若∠A=60°,∠B=80°,则∠CDE的度数是( )| A、20° | B、30° |
| C、35° | D、40° |
为了了解我市17000名七年级学生上学期期末数学考试的成绩情况,从中抽取了200名学生的成绩进行统计.在这个问题中,下列说法:(1)这17000名学生的数学考试成绩的全体是总体;(2)每个学生是个体;(3)200名学生是总体的一个样本;(4)样本容量是200,其中正确的有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
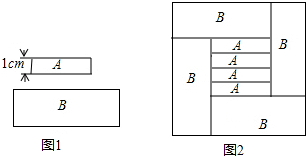 用A、B两种规格的长方形纸板(如图1)无重合无缝隙的拼接可得如图2所示的周长为32cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积是( )
用A、B两种规格的长方形纸板(如图1)无重合无缝隙的拼接可得如图2所示的周长为32cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积是( )| A、10cm2 |
| B、12cm2 |
| C、14cm2 |
| D、16cm2 |
 已知,如图,E在直线DF上,B在直线AC上,若∠AGB=∠EHF,∠C=∠D.求证:AC∥DF.(注明理由)
已知,如图,E在直线DF上,B在直线AC上,若∠AGB=∠EHF,∠C=∠D.求证:AC∥DF.(注明理由) 如图,CD∥AB,∠ABF=
如图,CD∥AB,∠ABF=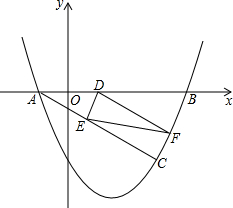 如图,已知抛物线y=
如图,已知抛物线y=