题目内容
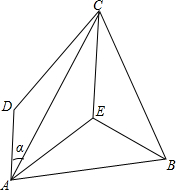 如图,在四边形ABCD中,BA=BC,AC是∠DAE的平分线,AD∥EC,∠AEB=120°.求∠DAC的度数α的值.
如图,在四边形ABCD中,BA=BC,AC是∠DAE的平分线,AD∥EC,∠AEB=120°.求∠DAC的度数α的值.考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:
分析:由已知AC是∠DAE的平分线可推出∠EAC=∠DAC,由DA∥CE可推出∠ECA=∠DAC,所以得到∠EAC=∠ECA,则AE=CE,又已知∠AEB=∠CEB,BE=BE,因此△AEB≌△CEB,问题得解.
解答:
解:∵AC是∠DAE的平分线,
∴∠DAC=∠CAE=α.
又∵DA∥EC,
∴∠DAC=∠ACE=α,
∴∠CAE=∠ACE=α,
∴AE=CE,∠AEC=180°-2α,
在△AEB和△CEB中,
,
∴△AEB≌△CEB(SSS),
∴∠AEB=∠CEB=120°,
∴∠AEC=360°-240°=120°,即180°-2α=120°.
解得 α=30°.

∴∠DAC=∠CAE=α.
又∵DA∥EC,
∴∠DAC=∠ACE=α,
∴∠CAE=∠ACE=α,
∴AE=CE,∠AEC=180°-2α,
在△AEB和△CEB中,
|
∴△AEB≌△CEB(SSS),
∴∠AEB=∠CEB=120°,
∴∠AEC=360°-240°=120°,即180°-2α=120°.
解得 α=30°.
点评:此题考查的知识点是平行线的性质、全等三角形的判定和性质,解答此题的关键是由已知先证明∠EAC=∠ECA,AE=CE,再证明△AEB≌△CEB.

练习册系列答案
相关题目
为了了解我市17000名七年级学生上学期期末数学考试的成绩情况,从中抽取了200名学生的成绩进行统计.在这个问题中,下列说法:(1)这17000名学生的数学考试成绩的全体是总体;(2)每个学生是个体;(3)200名学生是总体的一个样本;(4)样本容量是200,其中正确的有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
下列计算不正确的是( )
A、3
| ||||||||||
B、
| ||||||||||
C、(
| ||||||||||
| D、-13-8=-21 |
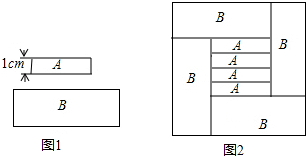 用A、B两种规格的长方形纸板(如图1)无重合无缝隙的拼接可得如图2所示的周长为32cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积是( )
用A、B两种规格的长方形纸板(如图1)无重合无缝隙的拼接可得如图2所示的周长为32cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积是( )| A、10cm2 |
| B、12cm2 |
| C、14cm2 |
| D、16cm2 |
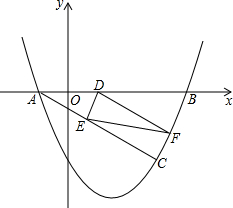 如图,已知抛物线y=
如图,已知抛物线y= 如图,在四边形ABCD中,∠1=∠2,∠3=∠4,∠B=∠D,AF=CE,AB∥CD.
如图,在四边形ABCD中,∠1=∠2,∠3=∠4,∠B=∠D,AF=CE,AB∥CD.