题目内容
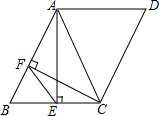 已知如图,在?ABCD中,∠D=60°,AE⊥BC,CF⊥AB,垂足分别为E,F.求证:AC=2EF.
已知如图,在?ABCD中,∠D=60°,AE⊥BC,CF⊥AB,垂足分别为E,F.求证:AC=2EF.考点:平行四边形的性质
专题:证明题
分析:利用相似三角形△BEF∽△BAC的对应边成比例得到:
=
=
=
,依此可得AC=2EF.
| BE |
| BA |
| BF |
| BC |
| EF |
| AC |
| 1 |
| 2 |
解答:
证明:∵四边形ABCD是平行四边形,∠D=60°,
∴∠D=∠B=60°.
又∵AE⊥BC,
∴在△ABE中,∠BAE=30°,
∴AB=2BE.
同理,在直角△BCF中,BC=2BF,
∴
=
=2.
又∵∠B是公共角,
∴△BEF∽△BAC,
∴
=
=
=
,
∴AC=2EF.
∴∠D=∠B=60°.
又∵AE⊥BC,
∴在△ABE中,∠BAE=30°,
∴AB=2BE.
同理,在直角△BCF中,BC=2BF,
∴
| AB |
| BE |
| BC |
| BF |
又∵∠B是公共角,
∴△BEF∽△BAC,
∴
| BE |
| BA |
| BF |
| BC |
| EF |
| AC |
| 1 |
| 2 |
∴AC=2EF.
点评:本题考查了平行四边形的性质.解题时,利用了含30度角的直角三角形的性质和相似三角形的判定与性质,难度不大.

练习册系列答案
相关题目
 如图,CD是△ABC的角平分线,DE∥BC.若∠A=60°,∠B=80°,则∠CDE的度数是( )
如图,CD是△ABC的角平分线,DE∥BC.若∠A=60°,∠B=80°,则∠CDE的度数是( )| A、20° | B、30° |
| C、35° | D、40° |
下列计算不正确的是( )
A、3
| ||||||||||
B、
| ||||||||||
C、(
| ||||||||||
| D、-13-8=-21 |
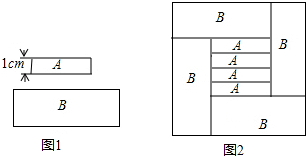 用A、B两种规格的长方形纸板(如图1)无重合无缝隙的拼接可得如图2所示的周长为32cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积是( )
用A、B两种规格的长方形纸板(如图1)无重合无缝隙的拼接可得如图2所示的周长为32cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积是( )| A、10cm2 |
| B、12cm2 |
| C、14cm2 |
| D、16cm2 |
二次函数y=x2-2x+m与x轴有交点,则m应满足的条件是( )
| A、m>1 | B、m≥1 |
| C、m<1 | D、m≤1 |
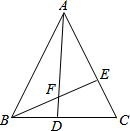 边长为4的等边△ABC,D,E分别在BC,AC上移动,D点从B运动到C,E从C运动到A.已知:D,E同时同速移动,连AD、BE交于F.
边长为4的等边△ABC,D,E分别在BC,AC上移动,D点从B运动到C,E从C运动到A.已知:D,E同时同速移动,连AD、BE交于F. △ABC是等边三角形,AB=8,AD是BC边上的高,DE⊥AC,求CE的长度.
△ABC是等边三角形,AB=8,AD是BC边上的高,DE⊥AC,求CE的长度. 如图,△ABC中,CD⊥AB于D,若AD=2BD,AC=6,BC=
如图,△ABC中,CD⊥AB于D,若AD=2BD,AC=6,BC=