题目内容
12.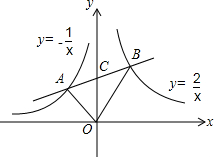 如图,已知直线AB与反比例函数$y=-\frac{1}{x}$和$y=\frac{2}{x}$交于A、B两点,与y轴交于点C,若AC=BC,则S△AOB=$\frac{3}{2}$.
如图,已知直线AB与反比例函数$y=-\frac{1}{x}$和$y=\frac{2}{x}$交于A、B两点,与y轴交于点C,若AC=BC,则S△AOB=$\frac{3}{2}$.
分析 作AD⊥y轴于D,BE⊥y轴于E,如图,先证明△ACD≌△BCE得到S△ACD=S△BCE,再利用面积代换得到S△AOB=S△AOD+S△BOE,然后根据反比例函数比例系数k的几何意义进行计算.
解答  解:作AD⊥y轴于D,BE⊥y轴于E,如图,
解:作AD⊥y轴于D,BE⊥y轴于E,如图,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{∠ADC=∠BEC}\\{∠ACD=∠BCE}\\{AC∠=BC}\end{array}\right.$,
∴△ACD≌△BCE,
∴S△ACD=S△BCE,
∴S△AOB=S△AOC+S△BOC
=S△AOD+S△ACD+S△BOC
=S△AOD+S△BCE+S△BOC
=S△AOD+S△BOE
=$\frac{1}{2}$•|-1|+$\frac{1}{2}$•|2|
=$\frac{3}{2}$.
故答案为$\frac{3}{2}$.
点评 本题考查了反比例函数与一次函数的交点问题:一次函数与反比例函数的交点坐标满足两个函数解析式.也考查了反比例函数比例系数k的几何意义.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
7. 如图,直线a∥b,∠1=50°,∠2=28°,则∠3的度数是( )
如图,直线a∥b,∠1=50°,∠2=28°,则∠3的度数是( )
 如图,直线a∥b,∠1=50°,∠2=28°,则∠3的度数是( )
如图,直线a∥b,∠1=50°,∠2=28°,则∠3的度数是( )| A. | 22° | B. | 28° | C. | 50° | D. | 30° |
 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑摩托车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人距B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑摩托车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人距B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: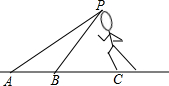 北京时间2008年8月16日晚上22:30,北京奥运会男子百米飞人大战在鸟巢打响,最终博尔特以9秒69的成绩打破世界纪录并轻松夺冠,博尔特再次打破人类历史,A,B两个镜头同时拍下了博尔特冲刺时的画面;从A镜头观测博尔特仰角为21°,从B镜头观测博尔特仰角为37°,已知AB=2.6米,你能根据上述信息计算出博尔特的身高吗?(sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$)
北京时间2008年8月16日晚上22:30,北京奥运会男子百米飞人大战在鸟巢打响,最终博尔特以9秒69的成绩打破世界纪录并轻松夺冠,博尔特再次打破人类历史,A,B两个镜头同时拍下了博尔特冲刺时的画面;从A镜头观测博尔特仰角为21°,从B镜头观测博尔特仰角为37°,已知AB=2.6米,你能根据上述信息计算出博尔特的身高吗?(sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$) 如图,方格纸中的每个小方格都是边长为1个单位的正方形,A(-6,1),B(-3,1),C(-3,3).△ABC绕点B顺时针旋转90°得到△A1BC1,请在图上画出△A1BC1的图形,并写出C1点坐标.
如图,方格纸中的每个小方格都是边长为1个单位的正方形,A(-6,1),B(-3,1),C(-3,3).△ABC绕点B顺时针旋转90°得到△A1BC1,请在图上画出△A1BC1的图形,并写出C1点坐标.