题目内容
17．对某条路线的长度进行n次测量，得到n个结果x1，x2，…，xn，在应用公式 s2=$\frac{1}{n}[{{{（{{x_1}-\overline x}）}^2}+{{（{{x_2}-\overline x}）}^2}+…+{{（{{x_n}-\overline x}）}^2}}]$计算方差时，$\overline x$是这n次测量结果的（ ）| A． | 平均数 | B． | 众数 | C． | 中位数 | D． | 最大值 |
分析 方差计算公式：S2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]，n表示样本容量，$\overline{x}$为平均数，根据此公式即可得到答案．
解答 解：在应用公式 s2=$\frac{1}{n}[{{{（{{x_1}-\overline x}）}^2}+{{（{{x_2}-\overline x}）}^2}+…+{{（{{x_n}-\overline x}）}^2}}]$计算方差时，$\overline x$是这n次测量结果的平均数，
故选A．
点评 此题主要考查了方差：一组数据中各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差．计算公式为：S2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]，其中n表示样本容量，x1，x2，…xn表示样本数据，$\overline{x}$为平均数．
练习册系列答案
相关题目
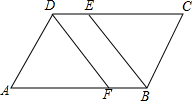已知，如图，在?ABCD中，∠ABC的平分线交CD于点E，∠ADC的平分线交AB于点F，求证：BF=DE．
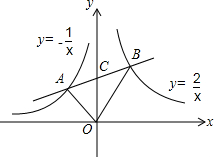如图，已知直线AB与反比例函数$y=-\frac{1}{x}$和$y=\frac{2}{x}$交于A、B两点，与y轴交于点C，若AC=BC，则S△AOB=$\frac{3}{2}$．
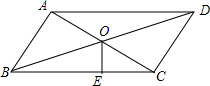如图，在平行四边形ABCD中，连接AC、BD，AD=5，BD=2$\sqrt{10}$，tan∠DBC=$\frac{1}{3}$，则平行四边形ABCD的面积是10．