题目内容
3. 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑摩托车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人距B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑摩托车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人距B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:(1)写出A、B两地之间的距离;
(2)请问甲乙两人何时相遇;
(3)求出在9-18小时之间甲乙两人相距s与时间x的函数表达式.
分析 (1)由函数图象可以得出A、B两地之间的距离为360km;
(2)根据函数图象可知,甲骑自行车从A地到B地需18小时,行驶360km,根据速度=路程÷时间求出甲的速度;乙骑摩托车从B地到A地需9小时,行驶360km,根据速度=路程÷时间求出乙的速度;再根据相遇问题的相等关系可得甲乙两人相遇时间;
(3)根据甲乙两人的速度求出在9-18小时之间,甲乙两人分别与A的距离为S甲=20x,S乙=40(x-9)=40x-360,根据s=S甲-S乙,即可求出s与时间x的函数表达式.
解答 解:(1)由题意的AB两地相距360米;
(2)由图得,V甲=360÷18=20km/h,V乙=360÷9=40km/h,
则t=360÷(20+40)=6h;
(3)在9-18小时之间,甲乙两人分别与A的距离为S甲=20x,S乙=40(x-9)=40x-360,
则s=S甲-S乙=360-20x.
点评 本题考查了一次函数的运用,相遇问题数量关系的运用,路程、速度与时间关系的运用,解答时认真分析函数图象,弄清函数图象的意义是关键.

练习册系列答案
相关题目
14.一组数据6,x,8,10,16的平均数为10,则这组数据的众数、中位数分别是( )
| A. | 10,16 | B. | 8,10 | C. | 10,12 | D. | 10,10 |
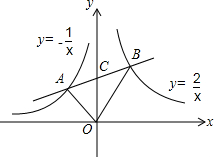 如图,已知直线AB与反比例函数$y=-\frac{1}{x}$和$y=\frac{2}{x}$交于A、B两点,与y轴交于点C,若AC=BC,则S△AOB=$\frac{3}{2}$.
如图,已知直线AB与反比例函数$y=-\frac{1}{x}$和$y=\frac{2}{x}$交于A、B两点,与y轴交于点C,若AC=BC,则S△AOB=$\frac{3}{2}$.