题目内容
已知一元二次方程x2+px+q+1=0的一个根为2
(1)求q关于p的关系式;
(2)求证:方程x2+px+q=0有两个不等的实数根;
(3)若方程x2+px+q+1=0有两个相等的实数根,求方程x2+px+q=0两根.
(1)求q关于p的关系式;
(2)求证:方程x2+px+q=0有两个不等的实数根;
(3)若方程x2+px+q+1=0有两个相等的实数根,求方程x2+px+q=0两根.
考点:根的判别式,一元二次方程的解
专题:
分析:(1)根据方程的解满足方程,把x=2代入已知方程,可得q关于p的关系式;
(2)根据方程有两个不等实数根,可得判别式大于零,根据解不等式,可得答案;
(3)根据方程有两个相等的实数根,可得判别式等于零,根据解方程组,可得p、q的值,根据因式分解法,可得方程的解.
(2)根据方程有两个不等实数根,可得判别式大于零,根据解不等式,可得答案;
(3)根据方程有两个相等的实数根,可得判别式等于零,根据解方程组,可得p、q的值,根据因式分解法,可得方程的解.
解答:解:(1)∵一元二次方程x2+px+q+1=0的一根为2,
∴4+2p+q+1=0,
∴q=-2p-5;
(2)∵x2+px+q=0,
∴△=p2-4q=p2-4(-2p-5)=(p+4)2+4>0,
∴方程x2+px+q=0有两个不等的实数根;
(3)x2+px+q+1=0有两个相等的实数根,
∴△=p2-4(q+1)=0,
由(1)可知q=-2p-5,
联立得方程组
,解得
,
把
代入x2+px+q=0,得
x2-4x+3=0,
因式分解,得
(x-1)(x-3)=0,
解得x1=1,x2=3.
∴4+2p+q+1=0,
∴q=-2p-5;
(2)∵x2+px+q=0,
∴△=p2-4q=p2-4(-2p-5)=(p+4)2+4>0,
∴方程x2+px+q=0有两个不等的实数根;
(3)x2+px+q+1=0有两个相等的实数根,
∴△=p2-4(q+1)=0,
由(1)可知q=-2p-5,
联立得方程组
|
|
把
|
x2-4x+3=0,
因式分解,得
(x-1)(x-3)=0,
解得x1=1,x2=3.
点评:本题考查了根的判别式,(1)方程的解满足方程,(2)利用了根的判别式,(3)解方程组,因式分解解方程.

练习册系列答案
相关题目
 如图,在等腰梯形ABCD中,AB∥CD,AD=BC,∠ACB=90°,∠B=60°,DC=2cm,求AB的长.
如图,在等腰梯形ABCD中,AB∥CD,AD=BC,∠ACB=90°,∠B=60°,DC=2cm,求AB的长.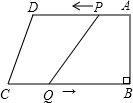 如图,已知梯形ABCD中,AD∥BC,∠B=90°,AD=21cm,BC=24cm,动点P从点A出发,以1cm/s的速度沿边AD向D运动,另一动点Q同时从C出发,以2cm/s的速度沿边CB向点B运动,其中一动点达到端点时,另一动点随之停止运动.设点P的运动时间为t秒.问:
如图,已知梯形ABCD中,AD∥BC,∠B=90°,AD=21cm,BC=24cm,动点P从点A出发,以1cm/s的速度沿边AD向D运动,另一动点Q同时从C出发,以2cm/s的速度沿边CB向点B运动,其中一动点达到端点时,另一动点随之停止运动.设点P的运动时间为t秒.问: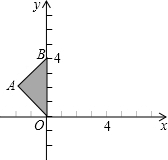 在平面直角坐标系中,等腰Rt△OAB斜边OB在y轴上,且OB=4.
在平面直角坐标系中,等腰Rt△OAB斜边OB在y轴上,且OB=4.