题目内容
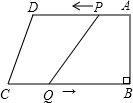 如图,已知梯形ABCD中,AD∥BC,∠B=90°,AD=21cm,BC=24cm,动点P从点A出发,以1cm/s的速度沿边AD向D运动,另一动点Q同时从C出发,以2cm/s的速度沿边CB向点B运动,其中一动点达到端点时,另一动点随之停止运动.设点P的运动时间为t秒.问:
如图,已知梯形ABCD中,AD∥BC,∠B=90°,AD=21cm,BC=24cm,动点P从点A出发,以1cm/s的速度沿边AD向D运动,另一动点Q同时从C出发,以2cm/s的速度沿边CB向点B运动,其中一动点达到端点时,另一动点随之停止运动.设点P的运动时间为t秒.问:(1)经过多少时间,四边形PQCD为平行四边形?
(2)经过多少时间,四边形PQBA为矩形?
(3)经过多少时间,四边形PQCD为等腰梯形?
考点:等腰梯形的判定,平行四边形的判定,矩形的判定
专题:动点型
分析:(1)四边形PQCD为平行四边形,即CQ=PD,列出方程求解即可;
(2)四边形PQCD为矩形,即AP=BQ,列出方程求解即可;
(3)四边形PQCD为等腰梯形,即CD=PQ,作梯形PQCD的高DE,PF,根据QC-PD=2CE列出方程求解即可.
(2)四边形PQCD为矩形,即AP=BQ,列出方程求解即可;
(3)四边形PQCD为等腰梯形,即CD=PQ,作梯形PQCD的高DE,PF,根据QC-PD=2CE列出方程求解即可.
解答: 解:设运动时间为t秒,
解:设运动时间为t秒,
∴AP=tcm,PD=AD-AP=(21-t)cm,CQ=2tcm,BQ=BC-CQ=(24-2t)cm.
(1)∵AD∥BC,
∴当CQ=PD时,四边形PQCD是平行四边形.
此时有2t=21-t,
解得t=7.
∴当t=7s时,四边形PQCD是平行四边形;
(2)∵AD∥BC,
∴当PA=BQ时,四边形PQBA是平行四边形,
∵∠B=90°,
∴四边形PQBA是矩形,
即t=24-2t,
解得:t=8,
∴t=8s时,四边形PQBA是矩形;
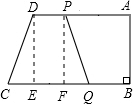 (3)当四边形PQCD为等腰梯形时,如图所示:
(3)当四边形PQCD为等腰梯形时,如图所示:
在Rt△PQF和Rt△DCE中,
,
∴Rt△PQF≌Rt△DCE(HL),
∴QF=CE,
∴QC-PD=QC-EF=QF+CE=2CE,即2t-(21-t)=6,
解得:t=9.
即当t=9s时,四边形PQCD为等腰梯形.
 解:设运动时间为t秒,
解:设运动时间为t秒,∴AP=tcm,PD=AD-AP=(21-t)cm,CQ=2tcm,BQ=BC-CQ=(24-2t)cm.
(1)∵AD∥BC,
∴当CQ=PD时,四边形PQCD是平行四边形.
此时有2t=21-t,
解得t=7.
∴当t=7s时,四边形PQCD是平行四边形;
(2)∵AD∥BC,
∴当PA=BQ时,四边形PQBA是平行四边形,
∵∠B=90°,
∴四边形PQBA是矩形,
即t=24-2t,
解得:t=8,
∴t=8s时,四边形PQBA是矩形;
 (3)当四边形PQCD为等腰梯形时,如图所示:
(3)当四边形PQCD为等腰梯形时,如图所示:在Rt△PQF和Rt△DCE中,
|
∴Rt△PQF≌Rt△DCE(HL),
∴QF=CE,
∴QC-PD=QC-EF=QF+CE=2CE,即2t-(21-t)=6,
解得:t=9.
即当t=9s时,四边形PQCD为等腰梯形.
点评:此题主要考查了矩形、平行四边形的判定,等腰梯形的判定与性质,利用数形结合与方程思想是解题的关键.

练习册系列答案
相关题目
计算50的结果为( )
| A、5 | B、0 | C、1 | D、无意义 |
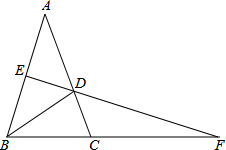 如图,在△ABC中,AB=AC,∠A=36°,BD是∠B的平分线,交AC于点D,E是AB中点,ED交BC的延长线于点F.求证:AB=CF.
如图,在△ABC中,AB=AC,∠A=36°,BD是∠B的平分线,交AC于点D,E是AB中点,ED交BC的延长线于点F.求证:AB=CF.