题目内容
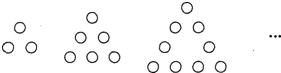
如图,由若干盆花组成形如三角形的图案,每条边(包括两个顶点)有n(n>1)盆花(图中用“○”表示),每个图案花盆的总数记为S.按此规律摆下去,以S、n为未知数的二元一次方程为 .

考点:由实际问题抽象出一元二次方程,规律型:图形的变化类
专题:
分析:由图可知:
第一图:有花盆3个,每条边有花盆2个,那么s=3×2-3;
第二图:有花盆6个,每条边有花盆3个,那么s=3×3-3;
第三图:有花盆9个,每条边有花盆4个,那么s=3×4-3;
…
由此可知以s,n为未知数的二元一次方程为s=3n-3.
第一图:有花盆3个,每条边有花盆2个,那么s=3×2-3;
第二图:有花盆6个,每条边有花盆3个,那么s=3×3-3;
第三图:有花盆9个,每条边有花盆4个,那么s=3×4-3;
…
由此可知以s,n为未知数的二元一次方程为s=3n-3.
解答:解:根据图案组成的是三角形的形状,则其周长等于边长的3倍,但由于每个顶点重复了一次.
所以s=3n-3.
故答案为s=3n-3.
所以s=3n-3.
故答案为s=3n-3.
点评:本题考查了规律型:图形的变化类,要注意给出的图片中所包含的规律,然后根据规律列出方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
小马虎在下面的计算中只做对了一道题,他做对的题是( )
| A、a2•a3=a6 |
| B、(a2)3=a6 |
| C、(-2a3)2=4a5 |
| D、a6÷a2=a3 |
计算50的结果为( )
| A、5 | B、0 | C、1 | D、无意义 |
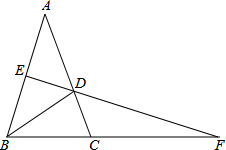 如图,在△ABC中,AB=AC,∠A=36°,BD是∠B的平分线,交AC于点D,E是AB中点,ED交BC的延长线于点F.求证:AB=CF.
如图,在△ABC中,AB=AC,∠A=36°,BD是∠B的平分线,交AC于点D,E是AB中点,ED交BC的延长线于点F.求证:AB=CF.