题目内容
已知a、b、c为△ABC的三边,且
+(b-c)2=0,试判断△ABC的形状.
| a2-b2-c2 |
考点:勾股定理的逆定理,非负数的性质:偶次方,非负数的性质:算术平方根,等腰直角三角形
专题:
分析:首先根据
+(b-c)2=0可得a2-b2-c2=0,且b-c=0,然后根据勾股定理逆定理可得△ABC的形状为等腰直角三角形.
| a2-b2-c2 |
解答:解:∵
+(b-c)2=0,
∴a2-b2-c2=0,且b-c=0,
∴a2=b2+c2,b=c,
∴△ABC的形状为等腰直角三角形.
| a2-b2-c2 |
∴a2-b2-c2=0,且b-c=0,
∴a2=b2+c2,b=c,
∴△ABC的形状为等腰直角三角形.
点评:此题主要考查了勾股定理逆定理以及非负数的性质,关键是掌握勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
给出四个数0,0.3,
,-
,其中最小的实数是( )
| 2 |
| 1 |
| 2 |
| A、0 | ||
| B、0.3 | ||
C、
| ||
D、-
|
 如图所示,Rt△ABC中,∠ACB=90°,∠BAC=45°,AD为∠BAC平分线交BC于E,BD⊥AD.求证:AE=2BD.
如图所示,Rt△ABC中,∠ACB=90°,∠BAC=45°,AD为∠BAC平分线交BC于E,BD⊥AD.求证:AE=2BD.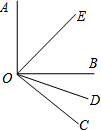 如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°.
如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°. 矩形ABCD的长AD=a,宽AB=b,E、F分别是AD、BC 上的点,BE、DF是相距为h的平行线,求AE的长(用a、b、h表示).
矩形ABCD的长AD=a,宽AB=b,E、F分别是AD、BC 上的点,BE、DF是相距为h的平行线,求AE的长(用a、b、h表示). 如图,在边长分别为9,12的矩形铁片中已经剪去两个半径都是3的⊙O1和⊙O2,如果要从残料上再剪一个⊙O3,求⊙O3的最大半径.
如图,在边长分别为9,12的矩形铁片中已经剪去两个半径都是3的⊙O1和⊙O2,如果要从残料上再剪一个⊙O3,求⊙O3的最大半径.