题目内容
填空：1+3=22，1+3+5=32，1+3+5+7=42，…从而猜想：1+3+5+…+2005= ．
考点：规律型：数字的变化类
专题：
分析：根据规律，从1开始的连续自然数的和等于奇数的个数的平方，然后求出奇数2005的序数，再平方即可．
解答：解：∵1+3=22，1+3+5=32，1+3+5+7=42，…，
2×1003-1=2005，
∴1+3+5+…+2005=20032．
故答案为：20032．
2×1003-1=2005，
∴1+3+5+…+2005=20032．
故答案为：20032．
点评：本题是对数字变化规律的考查，观察出从1开始的连续自然数的和等于奇数的个数的平方是解题的关键，难点在于求出奇数2005的序数．
练习册系列答案
相关题目
如图，在△ABC中，AB=AC，AD⊥BC，CE⊥AB，AD=12，CE=8，求S△ABC．
如图，已知PA、PB分别与⊙O相切于点A、B，点C在PB上，且CO∥PA，CD⊥PA于点D．
如图所示，Rt△ABC中，∠ACB=90°，∠BAC=45°，AD为∠BAC平分线交BC于E，BD⊥AD．求证：AE=2BD．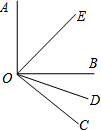
如图所示，OE和OD分别是∠AOB和∠BOC的平分线，且∠AOB=90°．
如图，在边长分别为9，12的矩形铁片中已经剪去两个半径都是3的⊙O1和⊙O2，如果要从残料上再剪一个⊙O3，求⊙O3的最大半径．