题目内容
4. 如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,则∠ADC=95°.
如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,则∠ADC=95°.
分析 首先由三角形的内角和定理求得∠C的度数,根据角平分线定义求出∠DAC,根据三角形内角和定理得出∠ADC=180°-∠DAC-∠C,代入求出即可.
解答 解:∵∠BAC=40°,∠B=75°,
∴∠C=180°-∠BAC-∠B=180°-40°-75°=65°,
∵AD平分∠CAB,∠BAC=40°,
∴∠DAC=$\frac{1}{2}$∠BAC=20°,
∴∠ADC=180°-∠DAC-∠C=180°-20°-65°=95°.
故答案为:95°.
点评 本题考查了三角形内角和定理,角平分线定义的应用,熟记三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
15.在一次抗震救灾中,某市组织20辆汽车装运食品、药品、生活用品三种救灾物资到灾民安置区,按计划每辆汽车只能装运一种救灾物资且必须装满.已知用了a辆汽车装运食品,用了b辆汽车装运药品,其余剩下的汽车装运生活用品,根据表中提供的信息,解答下列问题:
(1)20辆汽车共装载了多少吨救灾物资?
(2)装运这批救灾物资的总费用是多少元?
| 物资种类 | 食品 | 药品 | 生活用品 |
| 每辆汽车运载(吨) | 6 | 5 | 4 |
| 每吨所需运费(元) | 120 | 160 | 100 |
(2)装运这批救灾物资的总费用是多少元?
13.已知等腰三角形一边长等于4,一边长等于9,它的周长是( )
| A. | 17或22 | B. | 22 | C. | 17 | D. | 13 |
14.下列不能判断四边形ABCD是平行四边形的是( )
| A. | AB=CD,AD=BC | B. | AB∥CD,AD=BC | C. | AB∥CD,AD∥BC | D. | ∠A=∠C,∠B=∠D |
 一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.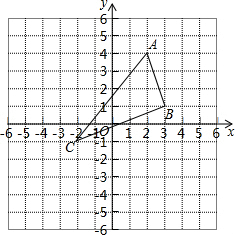 如图,在平面直角坐标系中,A(2,4),B(3,1),C(-2,-1).
如图,在平面直角坐标系中,A(2,4),B(3,1),C(-2,-1). 如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A,B两点,其中A点的坐标为(-3,0).
如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A,B两点,其中A点的坐标为(-3,0).