Question

9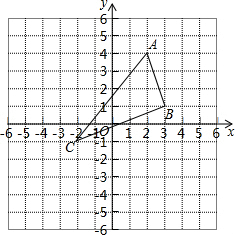．如图，在平面直角坐标系中，A（2，4），B（3，1），C（-2，-1）．
（1）求△ABC的面积；
（2）在图中作出△ABC关于x轴的对称图形△A₁B₁C₁，并写出点A₁，B₁，C₁的坐标．

Answer 1

分析 （1）直接利用△ABC所在矩形面积减去周围三角形面积进而得出答案；
（2）利用关于x轴对称点的性质得出对应点位置进而得出答案．

解答 解：（1）S_△ABC=5×5-$\frac{1}{2}$×4×5-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×5=$\frac{17}{2}$；

（2）如图所示：△A₁B₁C₁，即为所求，
A₁（2，-4），B₁（3，-1），C₁（-2，1）．

点评 此题主要考查了轴对称变换以及三角形面积求法，正确得出对应点位置是解题关键．