题目内容
12. 一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.(1)根据图中信息,可知甲乙两地之间的距离为280千米,两车出发2小时相遇;
(2)已知两车相遇时快车比慢车多行驶40千米,求快车从甲地到达乙地所需时间.
分析 (1)根据函数图象可以直接得到甲乙两地之间的距离和两车相遇的时间;
(2)根据题意可以求出慢车的速度,进而求得快车的速度,从而可以求得快车从甲地到达乙地所需时间.
解答 解:(1)由题意和图象可得,
甲乙两地之间的距离为280千米,两车出发2小时相遇,
故答案为:280,2;
(2)由题意可得,
慢车的速度为:$\frac{280-40}{4}=60$千米/时,
∴快车的速度为:60+(40÷2)=80千米/时,
∴快车从甲地到达乙地所需时间为:280÷80=3.5(小时),
即快车从甲地到达乙地所需时间是3.5小时.
点评 本题考查一次函数的应用,明确题意,利用数形结合的思想是解答本题的关键.

练习册系列答案
相关题目
7.已知点P(3,-2),则点P位于平面直角坐标系中的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17. 如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BC=4cm,CD=3cm,则点D到AB的距离是( )
如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BC=4cm,CD=3cm,则点D到AB的距离是( )
 如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BC=4cm,CD=3cm,则点D到AB的距离是( )
如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BC=4cm,CD=3cm,则点D到AB的距离是( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
2.我市某镇苹果大丰收,但因销路不畅,出现滞销,政府为解决果农困难,积极联系某公司购进一批苹果,已知购入苹果数量x与花费钱数y的关系如表,写出用x表示y的关系式y=6.1x+3.
| 数量x(千克) | 2 | 3 | 4 | 5 | … |
| 花费y(元) | 15.2 | 21.3 | 27.4 | 33.5 |
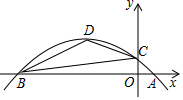 二次函数y=ax2+bx+c 的图象与x轴交于A(1,0),B两点,与y轴交于点C,其顶点D的坐标为(-3,2).
二次函数y=ax2+bx+c 的图象与x轴交于A(1,0),B两点,与y轴交于点C,其顶点D的坐标为(-3,2). 如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,则∠ADC=95°.
如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,则∠ADC=95°. 如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M的坐标为(8,10).
如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M的坐标为(8,10).