题目内容
6.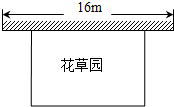 某中学课外兴趣活动小组准备围建一个矩形花草园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为16米(如图所示),设这个花草园垂直于墙的一边长为x米.
某中学课外兴趣活动小组准备围建一个矩形花草园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为16米(如图所示),设这个花草园垂直于墙的一边长为x米.(1)若花草园的面积为100平方米,求x;
(2)若平行于墙的一边长不小于10米,这个花草园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个花草园的面积不小于88平方米时,直接写出x的取值范围.
分析 (1)根据题意得方程求解即可;
(2)设苗圃园的面积为y,根据题意得到二次函数解析式y=x(30-2x)=-2x2+30x,根据二次函数的性质求解即可;
(3)由题意得不等式,即可得到结论.
解答 解:(1)根据题意知平行于墙的一边的长为(30-2x)米,
则有:x(30-2x)=100,
解得:x=5或x=10,
∵0<30-2x≤16,
∴7≤x<15,
故x=10;
(2)设苗圃园的面积为y,
∴y=x(30-2x)=-2x2+30x,
∵a=-2<0,
∴苗圃园的面积y有最大值,
∵30-2x≥10,
解得:x≤10,
∴7≤x≤10,
∴当x=$\frac{15}{2}$时,即平行于墙的一边长15>10米,y最大=112.5平方米;
当x=10时,y最小=100;
(3)由题意得-2x2+30x≥88,
解得:x≤4或x≥11,
又∵7≤x<15,
∴11≤x<15.
点评 此题考查了二次函数、一元二次方程、一元二次不等式的实际应用问题.解题的关键是根据题意构建二次函数模型,然后根据二次函数的性质求解即可.

练习册系列答案
相关题目
17.如图所示,四个三角形,能构成全等三角形的是( )


| A. | ②和③ | B. | ②和④ | C. | ①和② | D. | ③和④ |
11.下列叙述正确的是( )
| A. | 有理数中有最大的数 | B. | 零是整数中最小的数 | ||
| C. | 有理数中有绝对值最小的数 | D. | 任何数的绝对值一定是正数 |
15.关于“0”的说法中正确的是( )
| A. | 0是最小的整数 | B. | 0是负数,也是自然数 | ||
| C. | 0是正数也是有理数 | D. | 0既不是正数,也不是负数 |
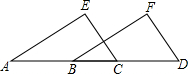 已知:如图点A、B、C、D在一条直线上,EA∥FB,EC∥FD,AB=CD,求证:EA=FB.
已知:如图点A、B、C、D在一条直线上,EA∥FB,EC∥FD,AB=CD,求证:EA=FB.