题目内容
3.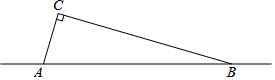 在公路AB旁有一座山,现山脚的C处需要爆破,已知点C与公路上的停靠站A的距离是700米,与公路上另一停靠站B的距离为2400米,且CA垂直于CB,为了安全起见,爆破点C周围半径680米范围内不得进入.请问在爆破时,公路AB段是否因有危险而需要暂时封锁?
在公路AB旁有一座山,现山脚的C处需要爆破,已知点C与公路上的停靠站A的距离是700米,与公路上另一停靠站B的距离为2400米,且CA垂直于CB,为了安全起见,爆破点C周围半径680米范围内不得进入.请问在爆破时,公路AB段是否因有危险而需要暂时封锁?
分析 如图,本题需要判断点C到AB的距离是否小于680米,如果小于则有危险,大于则没有危险.因此过C作CD⊥AB于D,然后根据勾股定理在直角三角形ABC中即可求出AB的长度,然后利用三角形的公式即可求出CD,然后和680米比较大小即可判断需要暂时封锁.
解答  解:如图,过C作CD⊥AB于D,
解:如图,过C作CD⊥AB于D,
∵BC=2400米,AC=700米,∠ACB=90°,
∴根据勾股定理得AB=2500米,
∵$\frac{1}{2}$AB•CD=$\frac{1}{2}$BC•AC,
∴CD=672米.
∵672米<680米,故有危险,
因此AB段公路需要暂时封锁.
点评 本题考查正确运用勾股定理,善于观察题目的信息是解题以及学好数学的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下列叙述正确的是( )
| A. | 有理数中有最大的数 | B. | 零是整数中最小的数 | ||
| C. | 有理数中有绝对值最小的数 | D. | 任何数的绝对值一定是正数 |
15.关于“0”的说法中正确的是( )
| A. | 0是最小的整数 | B. | 0是负数,也是自然数 | ||
| C. | 0是正数也是有理数 | D. | 0既不是正数,也不是负数 |
 已知,如图,在△ABC中,AC>BC,B=45°,点D是AB的中点,CE⊥AB于点E.
已知,如图,在△ABC中,AC>BC,B=45°,点D是AB的中点,CE⊥AB于点E.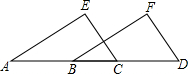 已知:如图点A、B、C、D在一条直线上,EA∥FB,EC∥FD,AB=CD,求证:EA=FB.
已知:如图点A、B、C、D在一条直线上,EA∥FB,EC∥FD,AB=CD,求证:EA=FB.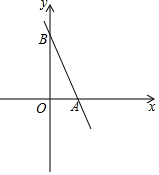 如图,直线y=-2x+3与x轴相交于点A,与y轴相交于点B.
如图,直线y=-2x+3与x轴相交于点A,与y轴相交于点B.