题目内容
10.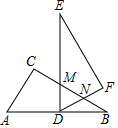 如图,Rt△ACB≌Rt△DFE,∠ACB=∠DFE=90°,D点在AB边的中点处,DE⊥AB,交BC边于点M,DF交BC边于点N,若∠B=∠E=30°,AC=3$\sqrt{3}$,则MN的长为( )
如图,Rt△ACB≌Rt△DFE,∠ACB=∠DFE=90°,D点在AB边的中点处,DE⊥AB,交BC边于点M,DF交BC边于点N,若∠B=∠E=30°,AC=3$\sqrt{3}$,则MN的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先根据含30°角的直角三角形的性质,得到AB=6$\sqrt{3}$,这个D点在AB边的中点处,得到BD=3$\sqrt{3}$,进而得出DM的长,再判定△MND是等边三角形,即可得出MN的长.
解答 解:如图,∵Rt△ACB中,∠B=30°,AC=3$\sqrt{3}$,
∴AB=6$\sqrt{3}$,
∵D点在AB边的中点处,
∴BD=3$\sqrt{3}$,
∵DE⊥AB,
∴DM=BD×tan∠ABC=3$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=3,
∵Rt△ACB≌Rt△DFE,∠B=∠E=30°,
∴∠BMD=∠EDF=60°,
∴∠MND=60°,
∴MN=MD=3,
故选:C.
点评 本题主要考查了全等三角形的性质以及含30°角的直角三角形的性质,解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
20.某商场计划购进A,B两种新型节能台灯共100盏,这两种节能台灯的进价和售价如下表所示:设购进A型台灯x盏,销售完这100盏台灯共获利润y元.
(1)求y与x的函数表达式.
(2)若商场预计进货款为3500元,求销售完这两种台灯的利润.
| 进价(元/盏) | 售价(元/盏) | |
| A | 30 | 45 |
| B | 50 | 70 |
(2)若商场预计进货款为3500元,求销售完这两种台灯的利润.
 如图,直线y=ax+b与x轴交于A,与y轴交于B,与双曲线y=$\frac{k}{x}$交于点C,D,OA=2OB=2.△OAB与△OAD的面积相等.
如图,直线y=ax+b与x轴交于A,与y轴交于B,与双曲线y=$\frac{k}{x}$交于点C,D,OA=2OB=2.△OAB与△OAD的面积相等.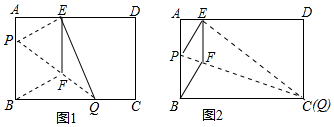
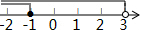
 已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:
已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:


 如图:在等腰Rt△ABC中,BD=AE,BF与DE垂直,求证:ED=BF.
如图:在等腰Rt△ABC中,BD=AE,BF与DE垂直,求证:ED=BF.