题目内容
2.已知,菱形ABCD的边长为5,菱形的面积为20,则对角线AC的长为4$\sqrt{5}$或2$\sqrt{5}$.分析 根据菱形的性质、菱形面积公式结合勾股定理得出BO的长,进而求出答案.
解答  解:依题意得:$\left\{\begin{array}{l}{2OA•OB=20}\\{O{A}^{2}+O{B}^{2}={5}^{2}}\end{array}\right.$,
解:依题意得:$\left\{\begin{array}{l}{2OA•OB=20}\\{O{A}^{2}+O{B}^{2}={5}^{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{OA=2\sqrt{5}}\\{OB=\sqrt{5}}\end{array}\right.$或$\left\{\begin{array}{l}{OB=2\sqrt{5}}\\{OA=\sqrt{5}}\end{array}\right.$.
故AC=2OA=4$\sqrt{5}$或AC=2OA=2$\sqrt{5}$.
故答案是:4$\sqrt{5}$或2$\sqrt{5}$.
点评 此题主要考查了菱形的性质以及勾股定理,正确掌握菱形的性质是解题关键.

练习册系列答案
相关题目
12.下列运算正确的是( )
| A. | x3+2x=3x4 | B. | x8+x2=x10 | C. | (-x)4•x2=x6 | D. | (-x5)2=-x10 |
10.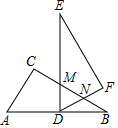 如图,Rt△ACB≌Rt△DFE,∠ACB=∠DFE=90°,D点在AB边的中点处,DE⊥AB,交BC边于点M,DF交BC边于点N,若∠B=∠E=30°,AC=3$\sqrt{3}$,则MN的长为( )
如图,Rt△ACB≌Rt△DFE,∠ACB=∠DFE=90°,D点在AB边的中点处,DE⊥AB,交BC边于点M,DF交BC边于点N,若∠B=∠E=30°,AC=3$\sqrt{3}$,则MN的长为( )
 如图,Rt△ACB≌Rt△DFE,∠ACB=∠DFE=90°,D点在AB边的中点处,DE⊥AB,交BC边于点M,DF交BC边于点N,若∠B=∠E=30°,AC=3$\sqrt{3}$,则MN的长为( )
如图,Rt△ACB≌Rt△DFE,∠ACB=∠DFE=90°,D点在AB边的中点处,DE⊥AB,交BC边于点M,DF交BC边于点N,若∠B=∠E=30°,AC=3$\sqrt{3}$,则MN的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.如果分式$\frac{x}{x+1}$没有意义,那么x的取值范围是( )
| A. | x≠0 | B. | x=0 | C. | x≠1 | D. | x=-1 |
 如图,在四边形ABCD中,AB=CD,AD=BC,点O为BD上任意一点,过点O的直线分别交AD,BC于M,N两点.求证:∠1=∠2.
如图,在四边形ABCD中,AB=CD,AD=BC,点O为BD上任意一点,过点O的直线分别交AD,BC于M,N两点.求证:∠1=∠2.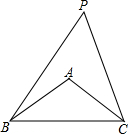 如图,在△ABC中,AB=AC=5,BC=8.若∠A=2∠P,则tan∠P=$\frac{4}{3}$.
如图,在△ABC中,AB=AC=5,BC=8.若∠A=2∠P,则tan∠P=$\frac{4}{3}$.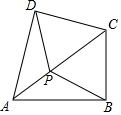 如图,在四边形ABCD中,AB=AD,∠ABC=∠ADC=90°,P为对角线AC上任一点,求证:PB=PD.
如图,在四边形ABCD中,AB=AD,∠ABC=∠ADC=90°,P为对角线AC上任一点,求证:PB=PD.