题目内容
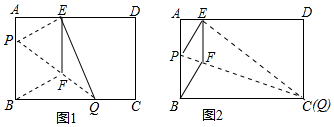
18.如图1,在矩形纸片ABCD中,AB=6cm,AD=10cm,折叠纸片使B点落在边AD上的点E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.
③以F为圆心,EF长为半径作⊙F,若⊙F与矩形ABCD的两边同时相切,求此时AE的长.
分析 (1)根据一组对边平行且相等可证得:四边形BFEP为平行四边形,再加上PB=PE可得结论;
(2)①先由折叠得:EC=BC=10,利用勾股定理得:ED=8,设PE=x,则PB=x,AP=6-x,Rt△APE中,由勾股定理得:(6-x)2+22=x2,解出即可;
②当点Q与点C重合时,点E离点A最近,由①知,此时AE=2cm;当点P与点A重合时,点E离点A最远,AE=AB=6cm,即可得出答案;
③当P与A重合,F与Q重合时,⊙F与AB和AD相切,如图4,根据图形得出AE的长.
解答 证明:(1)如图1,由折叠得:BP=PE,∠BPF=∠EPF,
∵EF∥AB,
∴∠BPF=∠PFE,
∴∠EPF=∠PFE,
∴PE=EF,
∴PB=EF,
∴四边形BFEP为平行四边形;
∵PB=PE,
∴四边形BFEP为菱形;
(2)①如图2,由折叠得:EC=BC=10,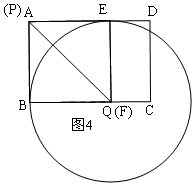
∵四边形ABCD平行四边形,
∴DC=AB=6,∠D=90°,
Rt△EDC中,ED=8,
∴AE=10-8=2,
设PE=x,则PB=x,AP=6-x,
Rt△APE中,由勾股定理得:(6-x)2+22=x2,
12x=40,
x=$\frac{10}{3}$;
∴PE=$\frac{10}{3}$,
∴菱形BFEP的边长是$\frac{10}{3}$cm;
②当点Q与点C重合时,如图2:
点E离点A最近,由①知,此时AE=2cm;
当点P与点A重合时,如图3所示:
点E离点A最远,此时四边形ABQE为正方形,AE=AB=6cm,
∴点E在边AD上移动的最大距离为4cm.
③当P与A重合,F与Q重合时,⊙F与AB和AD相切,如图4,
此时AE=AB=6cm.
点评 本题是四边形综合题目,考查了矩形的性质、折叠的性质、菱形的判定、平行线的性质、等腰三角形的判定、勾股定理、正方形的性质等知识;本题综合性强,有一定难度.

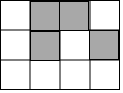 如图,在4×3长方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
如图,在4×3长方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |

那么下面四个数中,满足上述共有性质的一个是( )
| A. | 228 | B. | 707 | C. | 808 | D. | 609 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
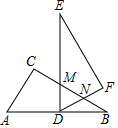 如图,Rt△ACB≌Rt△DFE,∠ACB=∠DFE=90°,D点在AB边的中点处,DE⊥AB,交BC边于点M,DF交BC边于点N,若∠B=∠E=30°,AC=3$\sqrt{3}$,则MN的长为( )
如图,Rt△ACB≌Rt△DFE,∠ACB=∠DFE=90°,D点在AB边的中点处,DE⊥AB,交BC边于点M,DF交BC边于点N,若∠B=∠E=30°,AC=3$\sqrt{3}$,则MN的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
 小明驾车从甲地到乙地,设他出发的速度与时间的函数图象如图所示下列四种说法:
小明驾车从甲地到乙地,设他出发的速度与时间的函数图象如图所示下列四种说法: