题目内容
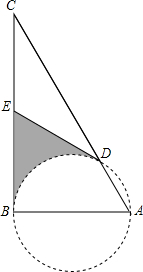 如图,AB为⊙O的直径,BC为⊙O的切线,连接AC交⊙O于D点,E为BC的中点,连接DE.
如图,AB为⊙O的直径,BC为⊙O的切线,连接AC交⊙O于D点,E为BC的中点,连接DE.(1)求证:DE为⊙O的切线;
(2)若∠A=60°,AD=2,求图中阴影部分的面积.
考点:切线的判定与性质,扇形面积的计算
专题:
分析:(1)先连接OD和BD,根据切线的性质求出∠ABC=90°,根据三角形中位线性质求出OE∥AC,根据平行线的性质推出∠EOB=∠A,∠EOD=∠ODA,进而求得∠EOB=∠EOD,然后根据SAS求得△OBE≌△ODE(SAS),证得∠ODE=∠ABC=90°,根据切线的判定推出即可.
(2)先求得△ODA是等边三角形,从而求得∠BOD=2∠A=120°,根据三角形全等的性质求得∠EOB=∠EOD=60°,进而求得∠OED=30°,根据30°的直角三角形的性质求得OE=2OD=4,EB=ED=
=2
,然后根据S阴影=S△BOE+S△DOE-S扇形OBD就可求得.
(2)先求得△ODA是等边三角形,从而求得∠BOD=2∠A=120°,根据三角形全等的性质求得∠EOB=∠EOD=60°,进而求得∠OED=30°,根据30°的直角三角形的性质求得OE=2OD=4,EB=ED=
| 42-22 |
| 3 |
解答: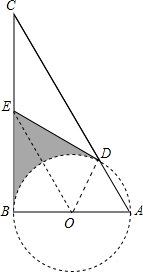 证明:(1)连接OD,OE,
证明:(1)连接OD,OE,
∵AB是⊙O的直径,BC为⊙O的切线,
∴∠ABC=90°,
∵E为BC的中点,OA=OB,
∴OE∥AC,
∴∠EOB=∠A,∠EOD=∠ODA,
∵OA=OB,
∴∠ODA=∠A,
∴∠EOB=∠EOD,
在△OBE和△ODE中,
,
∴△OBE≌△ODE(SAS),
∴∠ODE=∠ABC=90°,
∴DE是⊙O的切线.
(2)∵OA=OD,∠A=60°,
∴△ODA是等边三角形,
∴∠BOD=2∠A=120°,
∴∠EOB=∠EOD=60°,
∵∠ODE=90°,
∴∠OED=30°,
∴OE=2OD=4,EB=ED=
=2
,
∴S阴影=S△BOE+S△DOE-S扇形OBD=
×2×2
+
×2×2
-
=
.
 证明:(1)连接OD,OE,
证明:(1)连接OD,OE,∵AB是⊙O的直径,BC为⊙O的切线,
∴∠ABC=90°,
∵E为BC的中点,OA=OB,
∴OE∥AC,
∴∠EOB=∠A,∠EOD=∠ODA,
∵OA=OB,
∴∠ODA=∠A,
∴∠EOB=∠EOD,
在△OBE和△ODE中,
|
∴△OBE≌△ODE(SAS),
∴∠ODE=∠ABC=90°,
∴DE是⊙O的切线.
(2)∵OA=OD,∠A=60°,
∴△ODA是等边三角形,
∴∠BOD=2∠A=120°,
∴∠EOB=∠EOD=60°,
∵∠ODE=90°,
∴∠OED=30°,
∴OE=2OD=4,EB=ED=
| 42-22 |
| 3 |
∴S阴影=S△BOE+S△DOE-S扇形OBD=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 120π×22 |
| 360 |
12
| ||
| 3 |
点评:本题考查了切线的判定,直角三角形的性质,三角形全等的判定,解此题的关键是求出∠ODE=90°,注意:经过半径的外端,并且垂直于这条半径的直线是圆的切线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,轮船C在观测站A的北偏东60°方向,在观测站B的北偏西45°方向,则从轮船C看A、B两站的视角∠ACB=( )
如图,轮船C在观测站A的北偏东60°方向,在观测站B的北偏西45°方向,则从轮船C看A、B两站的视角∠ACB=( )| A、105° | B、100° |
| C、120° | D、110° |
抛物线y=-x2+x-1与坐标轴(含x轴、y轴)的公共点的个数是( )
| A、0 | B、1 | C、2 | D、3 |
在Rt△ABC中,∠C=90°,如果∠A=α,AB=c,那么BC等于( )
| A、c•sinα |
| B、c•cosα |
| C、c•tanα |
| D、c•cotα |
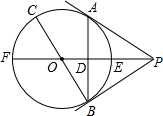 如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,F,过点A作PO的垂线AB,垂足为D,交⊙O于点B,BO的延长线交⊙O于点C.
如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,F,过点A作PO的垂线AB,垂足为D,交⊙O于点B,BO的延长线交⊙O于点C. 小明、小亮做一个“配色”的游戏.下图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,或者转盘A转出了蓝色,转盘B转出了红色,则红色和蓝色在一起配成紫色.这种情况下小亮得1分;同样,蓝色和黄色在一起配成绿色,这种情况下小明得1分;在其它情况下,则小明、小亮不分胜负.这个游戏对双方公平吗?请说明理由.若不公平,如何修改游戏规则才能使游戏对双方公平?
小明、小亮做一个“配色”的游戏.下图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,或者转盘A转出了蓝色,转盘B转出了红色,则红色和蓝色在一起配成紫色.这种情况下小亮得1分;同样,蓝色和黄色在一起配成绿色,这种情况下小明得1分;在其它情况下,则小明、小亮不分胜负.这个游戏对双方公平吗?请说明理由.若不公平,如何修改游戏规则才能使游戏对双方公平?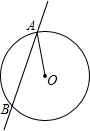 如图,已知直线AB与⊙O相交于A、B两点,∠OAB=30°,半径OA=2,那么弦AB=
如图,已知直线AB与⊙O相交于A、B两点,∠OAB=30°,半径OA=2,那么弦AB=