题目内容
已知抛物线y=ax2+bx+c与x轴的两个交点分别为(-1,0),(-5,0),那么一元二次方程ax2+bx+c=0的根为 .
考点:抛物线与x轴的交点
专题:计算题
分析:根据抛物线与x轴的交点问题,两交点的横坐标即为方程ax2+bx+c=0的解.
解答:解:∵抛物线y=ax2+bx+c与x轴的两个交点分别为(-1,0),(-5,0),
即自变量为-1和-5时函数值为0,
∴一元二次方程ax2+bx+c=0的根为x1=-1,x2=-5.
故答案为x1=-1,x2=-5.
故答案为x1=-1,x2=-5.
即自变量为-1和-5时函数值为0,
∴一元二次方程ax2+bx+c=0的根为x1=-1,x2=-5.
故答案为x1=-1,x2=-5.
故答案为x1=-1,x2=-5.
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
小明同学在“百度”搜索引擎中输入“中国梦,我的梦”,搜索到与之相关的结果条数约为91800000,把91800000这个数用科学记数法表示为( )
| A、918×103 |
| B、9.18×106 |
| C、9.18×107 |
| D、0.918×108 |
 二次函数y=(a-1)x2(a为常数)的图象如图所示,则a的取值范围为( )
二次函数y=(a-1)x2(a为常数)的图象如图所示,则a的取值范围为( )| A、a>1 | B、a<1 |
| C、a>0 | D、a<0 |
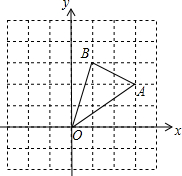 如图,在边长为1的正方形组成的网格中,△△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到A1OB1.
如图,在边长为1的正方形组成的网格中,△△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到A1OB1.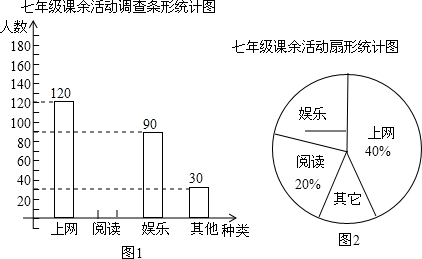

 如图,在亚丁湾海域护航的我国A、B两艘军舰在同一条航线上航行,它们同时收到一艘商船C的求救信号,A舰发现商船在它的北偏东30°方向上,B舰发现商船在它的北偏西60°方向上.
如图,在亚丁湾海域护航的我国A、B两艘军舰在同一条航线上航行,它们同时收到一艘商船C的求救信号,A舰发现商船在它的北偏东30°方向上,B舰发现商船在它的北偏西60°方向上.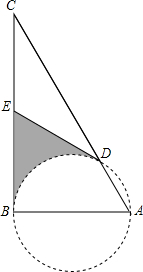 如图,AB为⊙O的直径,BC为⊙O的切线,连接AC交⊙O于D点,E为BC的中点,连接DE.
如图,AB为⊙O的直径,BC为⊙O的切线,连接AC交⊙O于D点,E为BC的中点,连接DE.