题目内容
在2,-2,0三个整数中,任取一个,恰好使分式
有意义的概率是 .
| 2+x |
| 2-x |
考点:概率公式,分式有意义的条件
专题:
分析:根据概率的求法,找准两点:
①全部情况的总数;
②符合条件的情况数目;二者的比值就是其发生的概率.
①全部情况的总数;
②符合条件的情况数目;二者的比值就是其发生的概率.
解答:解:∵在2,-2,0三个整数中,任取一个,恰好使分式
有意义的有-2,0,
∴使分式
有意义的概率为:
.
故答案为:
.
| 2+x |
| 2-x |
∴使分式
| 2+x |
| 2-x |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
估算
+2的值( )
| 24 |
| A、在5和6之间 |
| B、在8和9之间 |
| C、在7和8之间 |
| D、在6和7之间 |
抛物线y=2x2,y=-2x2,y=
x2共有的性质是( )
| 1 |
| 2 |
| A、开口向下 |
| B、对称轴是y轴 |
| C、都有最低点 |
| D、y的值随x的增大而减小 |
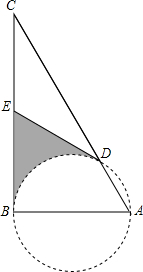 如图,AB为⊙O的直径,BC为⊙O的切线,连接AC交⊙O于D点,E为BC的中点,连接DE.
如图,AB为⊙O的直径,BC为⊙O的切线,连接AC交⊙O于D点,E为BC的中点,连接DE.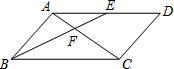 已知:如图,?ABCD中,E是AD中点,BE交AC于点F,设
已知:如图,?ABCD中,E是AD中点,BE交AC于点F,设 如图所示的运算程序中,若开始输入的x值为64,我们发现第一次输出的结果为32,第二次输出的结果为16,…,则第2013此输出的结果为( )
如图所示的运算程序中,若开始输入的x值为64,我们发现第一次输出的结果为32,第二次输出的结果为16,…,则第2013此输出的结果为( )