题目内容
在Rt△ABC中，∠C=90°，如果∠A=α，AB=c，那么BC等于（ ）
| A、c•sinα |
| B、c•cosα |
| C、c•tanα |
| D、c•cotα |
考点：锐角三角函数的定义
专题：
分析：根据题意画出图形，进而利用sinA=
，求出即可．
| BC |
| AB |
解答：
解：如图所示：∵在Rt△ABC中，∠C=90°，∠A=α，AB=c，
∴sinA=
，
∴BC=AB•sinA=c•sinα，
故选：A．
解：如图所示：∵在Rt△ABC中，∠C=90°，∠A=α，AB=c，∴sinA=
| BC |
| AB |
∴BC=AB•sinA=c•sinα，
故选：A．
点评：此题主要考查了锐角三角函数关系，正确记忆锐角三角函数关系是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
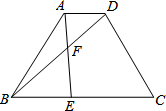如图，已知等腰梯形ABCD中，AD∥BC，AD=1，BC=3，AB=CD=2，点E在BC边上，AE与BD交于点F，∠BAE=∠DBC．
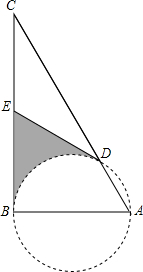如图，AB为⊙O的直径，BC为⊙O的切线，连接AC交⊙O于D点，E为BC的中点，连接DE．
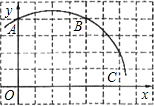如图，已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C．若A点的坐标为（0，4），D点的坐标为（7，0）．估算
+2的值（ ）
| 24 |
| A、在5和6之间 |
| B、在8和9之间 |
| C、在7和8之间 |
| D、在6和7之间 |
抛物线y=2x2，y=-2x2，y=
x2共有的性质是（ ）
| 1 |
| 2 |
| A、开口向下 |
| B、对称轴是y轴 |
| C、都有最低点 |
| D、y的值随x的增大而减小 |