题目内容
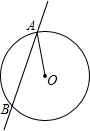 如图,已知直线AB与⊙O相交于A、B两点,∠OAB=30°,半径OA=2,那么弦AB=
如图,已知直线AB与⊙O相交于A、B两点,∠OAB=30°,半径OA=2,那么弦AB=考点:垂径定理,含30度角的直角三角形,勾股定理
专题:
分析:过O作OC⊥AB于C,根据垂直和垂径定理求出AB=2AC,∠OCA=90°,根据含30度角的直角三角形性质求出OC=1,根据勾股定理求出AC,即可得出答案.
解答:解:
过O作OC⊥AB于C,
则AB=2AC,∠OCA=90°,
∵OA=2,∠OAB=30°,
∴OC=1,由勾股定理得:AC=
=
,
∴AB=2AC=2
,
故答案为:2
.

过O作OC⊥AB于C,
则AB=2AC,∠OCA=90°,
∵OA=2,∠OAB=30°,
∴OC=1,由勾股定理得:AC=
| 22-12 |
| 3 |
∴AB=2AC=2
| 3 |
故答案为:2
| 3 |
点评:本题考查了垂径定理,含30度角的直角三角形性质,勾股定理的应用,解此题的关键是正确作出辅助线后求出AC的长和得出AB=2AC,注意:垂直于弦的直径平分这条弦.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知
=
,那么下列等式中,不一定正确的是( )
| a |
| b |
| 5 |
| 2 |
| A、2a=5b | ||||
B、
| ||||
| C、a+b=7 | ||||
D、
|
估算
+2的值( )
| 24 |
| A、在5和6之间 |
| B、在8和9之间 |
| C、在7和8之间 |
| D、在6和7之间 |
 如图,在亚丁湾海域护航的我国A、B两艘军舰在同一条航线上航行,它们同时收到一艘商船C的求救信号,A舰发现商船在它的北偏东30°方向上,B舰发现商船在它的北偏西60°方向上.
如图,在亚丁湾海域护航的我国A、B两艘军舰在同一条航线上航行,它们同时收到一艘商船C的求救信号,A舰发现商船在它的北偏东30°方向上,B舰发现商船在它的北偏西60°方向上.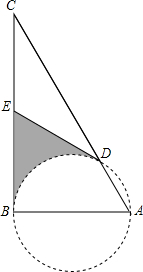 如图,AB为⊙O的直径,BC为⊙O的切线,连接AC交⊙O于D点,E为BC的中点,连接DE.
如图,AB为⊙O的直径,BC为⊙O的切线,连接AC交⊙O于D点,E为BC的中点,连接DE.