题目内容
1. 如图,AB是⊙O的直径,CD是⊙O的弦,若∠BAC=22°,则∠ADC的度数是68°.
如图,AB是⊙O的直径,CD是⊙O的弦,若∠BAC=22°,则∠ADC的度数是68°.
分析 根据直径所对的圆周角是直角求得∠ACB=90°,则根据直角三角形的性质求得∠ABC的度数,然后根据同弧所对的圆周角相等求解.
解答 解:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ABC=90°-∠BAC=90°-22°=68°.
∴∠ADC=∠ABC=68°.
故答案为:68°.
点评 本题考查了圆周角定理,理解定理的内容,由AB是直径得到∠ACB是直角是本题的关键.

练习册系列答案
相关题目
9.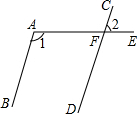 如图,AB∥CD,射线AE交CD于点F,若∠1=105°,则∠2的度数是( )
如图,AB∥CD,射线AE交CD于点F,若∠1=105°,则∠2的度数是( )
 如图,AB∥CD,射线AE交CD于点F,若∠1=105°,则∠2的度数是( )
如图,AB∥CD,射线AE交CD于点F,若∠1=105°,则∠2的度数是( )| A. | 75° | B. | 85° | C. | 95° | D. | 105° |
13.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{0.5}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{12}$ |
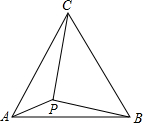 如图,△ABC为等边三角形,AB=2.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为$\frac{2\sqrt{3}}{3}$.
如图,△ABC为等边三角形,AB=2.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为$\frac{2\sqrt{3}}{3}$.