题目内容
6.(1)解不等式组:$\left\{\begin{array}{l}{3x-2≤x①}\\{\frac{2x+1}{5}<\frac{x+1}{2}②}\end{array}\right.$(2)解方程:$\frac{1-x}{2}$=$\frac{4x-1}{3}$-1.
分析 (1)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
(2)根据解一元一次方程基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.
解答 解:(1)解不等式①得:x≤1,
解不等式②得x>-3,
∴不等式组的解集是:-3<x≤1.
(2)方程两边同时乘以6,得:3(1-x)=2(4x-1)-6,
去括号,得:3-3x=8x-2-6,
移项,得:-3x-8x=-2-6-3,
合并同类项,得:-11x=-11,
系数化为1,得:x=1.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
14.下列关于正方形的叙述,正确的是( )
| A. | 正方形有且只有一个内切圆 | |
| B. | 正方形有无数个外接圆 | |
| C. | 对角线相等且垂直的四边形是正方形 | |
| D. | 用一根绳子围成一个平面图形,正方形的面积最大 |
16.估计$\sqrt{32}$-$\sqrt{16}$÷2的运算结果在哪两个整数之间( )
| A. | 0和1 | B. | 1和2 | C. | 2和3 | D. | 3和4 |

 如图,AB是⊙O的直径,CD是⊙O的弦,若∠BAC=22°,则∠ADC的度数是68°.
如图,AB是⊙O的直径,CD是⊙O的弦,若∠BAC=22°,则∠ADC的度数是68°.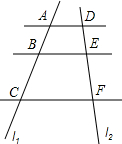 如图,直线AD∥BE∥CF,它们分别交直线l1、l2于点A、B、C和点D、E、F.若AB=2,BC=4,则$\frac{DE}{DF}$的值为$\frac{1}{3}$.
如图,直线AD∥BE∥CF,它们分别交直线l1、l2于点A、B、C和点D、E、F.若AB=2,BC=4,则$\frac{DE}{DF}$的值为$\frac{1}{3}$.