题目内容
11.如图1,菱形ABCD中,已知∠BAD=120°,∠EGF=60°,∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC,CD于点E,F.(1)如图2,当顶点G运动到与点A重合时,求证:EC+CF=BC;
(2)知识探究:①如图3,当顶点G运动到AC中点时,探究线段EC,CF与BC的数量关系;
②在顶点G的运动过程中,若$\frac{AC}{CG}$=t,请直接写出线段EC,CF与BC的数量关系(不需要写出证明过程);
(3)问题解决:如图4,已知菱形边长为8,BG=7,CF=$\frac{6}{5}$,当t>2时,求EC的长度.

分析 (1)如图2中,在CA上取一点M,使得CM=CE,连接EM.首先证明△ABE≌△ACF,再证明△AEM≌△FEC,即可解决问题.
(2)①结论:EC+CF=$\frac{1}{2}$BC.如图3中,取BC中点P,CD中点Q,连接PG、GQ.利用(1)的结论解决问题.
②结论:CE+CF=$\frac{BC}{t}$.如图4中,作GP∥AB交BC于P,GQ∥AD交CD于Q.利用(1)的结论解决问题.
(3)如图4中,作BM⊥AC于M.利用(1)的结论:CG=CE+CF,求出CE即可解决问题.
解答 (1)证明:如图2中,在CA上取一点M,使得CM=CE,连接EM.
∵四边形ABCD是菱形,∠BAD=120°,
∴AB=BC=CD=AD,∠CAB=∠CAD=60°,
∴△ABC,△ACD都是等边三角形,
∴∠AB=AC,∠BAC=∠EAF=60°,∠B=∠ACF=60°,
∴∠BAE=∠CAF,
在△BAE和△CAF中,$\left\{\begin{array}{l}{∠BAE=∠CAF}\\{∠B=∠ACF}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACF,
∴AE=AF,∵∠EAF=60°,
∴△AEF是等边三角形,
∵CE=CM,∠ECM=60°,
∴△ECM是等边三角形,
∴∠AEF=∠MEC=60°,AE=EF,EM=EC,
∴∠AEM=∠FEC,
在△AEM和△FEC中,
$\left\{\begin{array}{l}{AE=EF}\\{∠AEM=∠FEC}\\{EM=EC}\end{array}\right.$,
∴△AEM≌△FEC,
∴AM=CF,
∴BC=AC=AM+CM=EC+CF.
(2)①结论:EC+CF=$\frac{1}{2}$BC.
理由:如图3中,取BC中点P,CD中点Q,连接PG、GQ.
∵AG=GC,CPB,CQ=DQ,
∴PG∥AB,GQ∥QD,
∴∠CPG=∠B=60°,∠CGP=∠CAB=60°,
∴△CPG是等边三角形,同理可证△CQG是等边三角形,
由(1)可知,CE+CF=PC=$\frac{1}{2}$BC.
②结论:CE+CF=$\frac{BC}{t}$.
理由:如图4中,作GP∥AB交BC于P,GQ∥AD交CD于Q.
∴PG∥AB,GQ∥QD,
∴∠CPG=∠B=60°,∠CGP=∠CAB=60°,
∴△CPG是等边三角形,同理可证△CQG是等边三角形,
由(1)可知,CE+CF=PC=CG,
∵AC=BC=t•CG,
∴CE+CF=$\frac{BC}{t}$.
(3)如图4中,作BM⊥AC于M.
∵t>2,
∴点G在线段CM上,
在Rt△ABM中,∵∠BMC=90°,BM=$\frac{\sqrt{3}}{2}$×8=4$\sqrt{3}$,BG=7,
∴MG=$\sqrt{B{G}^{2}-B{M}^{2}}$=$\sqrt{{7}^{2}-(4\sqrt{3})^{2}}$=1,
∵CM=MA=4,
∴CG=CM-MG=3,
由(1)可知,CG=CE+CF,
∴CE=CG-CF=3-$\frac{6}{5}$=$\frac{9}{5}$.
点评 本题考查了相似形综合题、全等三角形的判定和性质、菱形的性质.等边三角形的判定和性质等知识,解题的关键是灵活运用这些知识解决问题,学会添加辅助线把问题转化为我们熟悉的图形,属于中考常考题型.

| A. | 0和1 | B. | 1和2 | C. | 2和3 | D. | 3和4 |
 如图,AB是⊙O的直径,CD是⊙O的弦,若∠BAC=22°,则∠ADC的度数是68°.
如图,AB是⊙O的直径,CD是⊙O的弦,若∠BAC=22°,则∠ADC的度数是68°. 如图,A、B、C为某公园的三个景点,景点A和景点B之间有一条笔直的小路,现要在小路上建一个凉亭P,使景点B、景点C到凉亭P的距离之和等于景点B到景点A的距离,请用直尺和圆规在所给的图中作出点P.(不写作法和证明,只保留作图痕迹)
如图,A、B、C为某公园的三个景点,景点A和景点B之间有一条笔直的小路,现要在小路上建一个凉亭P,使景点B、景点C到凉亭P的距离之和等于景点B到景点A的距离,请用直尺和圆规在所给的图中作出点P.(不写作法和证明,只保留作图痕迹)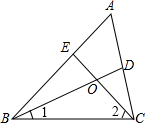 请从以下两个小题中任选一个作答,若多选,则按第一题计分.
请从以下两个小题中任选一个作答,若多选,则按第一题计分.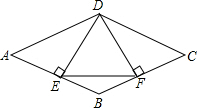 如图,在菱形ABCD中,过点D作DE⊥AB于点E,作DF⊥BC于点F,连接EF.
如图,在菱形ABCD中,过点D作DE⊥AB于点E,作DF⊥BC于点F,连接EF.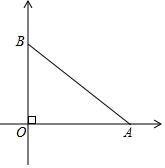 甲、乙两位探险者今年到沙漠进行探险,没有了水,需要寻找水源,为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为12千米,早晨8:00甲先出发,他以4千米/时的速度向东行走,1小时后乙出发,他以6千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?
甲、乙两位探险者今年到沙漠进行探险,没有了水,需要寻找水源,为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为12千米,早晨8:00甲先出发,他以4千米/时的速度向东行走,1小时后乙出发,他以6千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?