题目内容
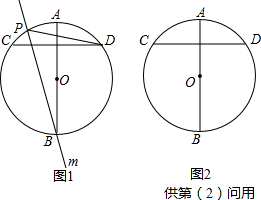
如图,在⊙O中直径AB垂直于弦CD(CD为非直径弦)有一直线m经过点B,且绕点B旋转交直线CD于E,交⊙O于P(P与D、B不重合).
(1)当直线BP如图1中的位置,试证明:①∠DPB=∠BDC,②BD2=BE•BP;
(2)当直线BP绕点B的旋转过程中,第(1)问的两个结论中有一个会出现不成立的情况,请你先画出该情况下的图形,再将不成立的那个等式给予纠正(也用等式表示),并给出证明.
(1)当直线BP如图1中的位置,试证明:①∠DPB=∠BDC,②BD2=BE•BP;
(2)当直线BP绕点B的旋转过程中,第(1)问的两个结论中有一个会出现不成立的情况,请你先画出该情况下的图形,再将不成立的那个等式给予纠正(也用等式表示),并给出证明.

考点:圆的综合题
专题:
分析:(1)利用垂径定理及推论得出
=
,以及利用相似三角形的判定与性质得出答案即可;
(2)利用圆周角定理以及其推论得出∠C所对的弧是
,∠DPB所对的弧为
,
+
刚好是一个圆,进而得出答案.
 |
| BC |
 |
| BD |
(2)利用圆周角定理以及其推论得出∠C所对的弧是
 |
| BD |
 |
| BCD |
 |
| BD |
 |
| BCD |
解答: (1)证明:连接BD,
(1)证明:连接BD,
∵直径AB⊥CD,
∴
=
,
∴∠BDC=∠BPD,
又∵∠DBP=∠EBD,
∴△PBD∽△DBE,
∴∠DPB=∠BDC,
∴
=
,
∴BD2=BE×PB;
(2)当点E在CD延长线上时,上问中结论①不成立,
正确的关系式是:∠BDC+∠DPB=180°,
证明:连接BC,BD,
∵∠C=∠BDC,
=
,
∴∠C所对的弧是
,∠DPB所对的弧为
,
+
刚好是一个圆,
∴∠C+∠DPB=180°,
即∠BDC+∠DPB=180°.
 (1)证明:连接BD,
(1)证明:连接BD,∵直径AB⊥CD,
∴
 |
| BC |
 |
| BD |
∴∠BDC=∠BPD,
又∵∠DBP=∠EBD,
∴△PBD∽△DBE,
∴∠DPB=∠BDC,
∴
| BD |
| BE |
| PB |
| DB |
∴BD2=BE×PB;
(2)当点E在CD延长线上时,上问中结论①不成立,
正确的关系式是:∠BDC+∠DPB=180°,
证明:连接BC,BD,
∵∠C=∠BDC,
 |
| BC |
 |
| BD |
∴∠C所对的弧是
 |
| BD |
 |
| BCD |
 |
| BD |
 |
| BCD |
∴∠C+∠DPB=180°,
即∠BDC+∠DPB=180°.
点评:此题主要考查了圆的综合应用以及圆周角定理以及推论和相似三角形的判定与性质等知识,得出△PBD∽△DBE是解题关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 (1)在平面直角坐标系中画出下列各点:A(-2,-3)、D(0,2)
(1)在平面直角坐标系中画出下列各点:A(-2,-3)、D(0,2)
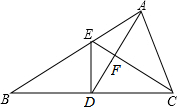 如图,已知在△ABC中,D是BC的中点,且AD=AC,DE⊥BC交AB于点E,EC与AD相交于点F.求证:AB•FD=AC•FC.
如图,已知在△ABC中,D是BC的中点,且AD=AC,DE⊥BC交AB于点E,EC与AD相交于点F.求证:AB•FD=AC•FC. 已知一个矩形的两邻边之比AB:AD=3:4,且周长为42cm,求矩形的对角线长.
已知一个矩形的两邻边之比AB:AD=3:4,且周长为42cm,求矩形的对角线长. 矩形ABCD的对角线交于点O,过点的直线分别交边AD、BC于N、M,求证:OM=ON.
矩形ABCD的对角线交于点O,过点的直线分别交边AD、BC于N、M,求证:OM=ON.