题目内容
已知B(2,0),C(8,0),A(0,a),若过A、B、C三点的圆面积最小,则a= .
考点:圆的综合题
专题:
分析:根据题意得出圆心在直线x=5上,进而利用半径最小时,则⊙M与y轴相切,A(0,a),进而利用勾股定理得出即可.
解答: 解:∵B(2,0),C(8,0),
解:∵B(2,0),C(8,0),
∴圆心在直线x=5上,
当过A、B、C三点的圆面积最小时,
则⊙M与y轴相切,A(0,a),
则圆心M(5,a),
|MA|=|MB|,
5=
,
解得:a=±4.
故答案为:±4.
 解:∵B(2,0),C(8,0),
解:∵B(2,0),C(8,0),∴圆心在直线x=5上,
当过A、B、C三点的圆面积最小时,
则⊙M与y轴相切,A(0,a),
则圆心M(5,a),
|MA|=|MB|,
5=
| 32+a2 |
解得:a=±4.
故答案为:±4.
点评:此题主要考查了圆的综合以及勾股定理和圆的性质等知识,利用圆的性质得出⊙M与y轴相切时过A、B、C三点的圆面积最小进而求出是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在正方形、矩形、菱形、平行四边形中,轴对称图形的有( )个.
| A、1 | B、2 | C、3 | D、4 |
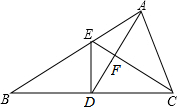 如图,已知在△ABC中,D是BC的中点,且AD=AC,DE⊥BC交AB于点E,EC与AD相交于点F.求证:AB•FD=AC•FC.
如图,已知在△ABC中,D是BC的中点,且AD=AC,DE⊥BC交AB于点E,EC与AD相交于点F.求证:AB•FD=AC•FC. 如图是甲、乙两人同一地点出发后,路程随时间变化的图象.
如图是甲、乙两人同一地点出发后,路程随时间变化的图象. 如图所示,已知A(1,y1),B(2,y2)为反比例函数y=
如图所示,已知A(1,y1),B(2,y2)为反比例函数y=