将抛物线y=x2向右平移2个单位所得抛物线的函数表达式为( )A．y=(x-2)2B．y=(x+2)2C．y=x2-2D．y=x2+2 题目和参考答案——青夏教育精英家教网—

题目内容

14．将抛物线y=x²向右平移2个单位所得抛物线的函数表达式为（　　）

A．

y=（x-2）²

B．

y=（x+2）²

C．

y=x²-2

D．

y=x²+2

分析易得原抛物线的顶点坐标，用顶点式表示出新的抛物线解析式，把新的顶点代入即可．

解答解：∵原抛物线的顶点为（0，0），把抛物线y=x²向右平移2个单位，
∴新抛物线的顶点为（2，0），
设新抛物线的解析式为y=（x-h）²+k，
∴所得抛物线的函数表达式为y=（x-2）²．
故选：A．

点评本题考查了二次函数的平移问题；用到的知识点为：平移不改变二次项的系数；平移看顶点的平移即可．

练习册系列答案

超能学典单元期中期末专题冲刺100分系列答案

A．

$\frac{1}{2}$ x（x-1）=45

B．

$\frac{1}{2}$ x（x+1）=45

5．某校成立“情暖校园”爱心基金会，去年上半年发给每个经济困难的学生600元，今年上半年发给了800元，设每半年发给的资金金额的平均增长率为x，则下面列出的方程中正确的是（　　）

2．

如图所示，AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3=（　　）

9．一个三边都是整数的三角形，其中两边长分别为1和2，第三边长是2

19．

如图，已知过原点的直线与双曲线$y=\frac{k}{x}$（k＞0）交于A、B两点，点A到x轴的距离是它到y轴距离的一半，点B的纵坐标为-2．
（1）求直线AB的解析式；
（2）求k的值；
（3）过原点O的另一条直线l交双曲线$y=\frac{k}{x}$（k＞0）于P，Q两点（点P在第一象限），若以A，B，P，Q为顶点的四边形面积为24，求点P的坐标．

6．已知，3＜m＜6，且点A（m，y₁），B（$\frac{1}{3}$m+1，y₂），C（2，y₃）都在二次函数y=$\sqrt{5}$x²-2$\sqrt{5}$x+3的图象上，则下列说法正确的是（　　）

y₂＜y₁＜y₃

y₂＜y₃＜y₁

y₃＜y₂＜y₁

y₁＜y₃＜y₂

11．

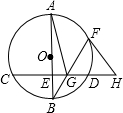如图．AB为⊙O的直径，CD为⊙O的弦，且AB⊥CD于E，F为劣弧$\widehat{AD}$上一点，BF交CD于点G，过点F作⊙O的切线，交CD的延长线于H．
（1）求证：FH=GH；
（2）若AB=2FH=10，GF=2$\sqrt{5}$，求AG的长．

12．

如图，已知抛物线与x轴交于A（-1，0）、B（5，0）两点，与y轴交于点C（0，5）．
（1）求该抛物线所对应的函数关系式；
（2）D是笫一象限内抛物线上的一个动点（与点C、B不重合），过点D作DF⊥x轴于点F，交直线BC于点E，连结BD、CD．设点D的横坐标为m，△BCD的面积为S．
①求S关于m的函数关系式及自变量m的取值范围；
②当m为何值时，S有最大值，并求这个最大值；
③直线BC能否把△BDF分成面积之比为2：3的两部分？若能，请求出点D的坐标；若不能，请说明理由．

试题分类