题目内容
11.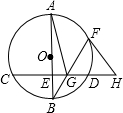 如图.AB为⊙O的直径,CD为⊙O的弦,且AB⊥CD于E,F为劣弧$\widehat{AD}$上一点,BF交CD于点G,过点F作⊙O的切线,交CD的延长线于H.
如图.AB为⊙O的直径,CD为⊙O的弦,且AB⊥CD于E,F为劣弧$\widehat{AD}$上一点,BF交CD于点G,过点F作⊙O的切线,交CD的延长线于H.(1)求证:FH=GH;
(2)若AB=2FH=10,GF=2$\sqrt{5}$,求AG的长.
分析 (1)如图,连接OF.由∠HFG+∠OFB=90°,OBF+∠EGB=90°,∠OBF=∠OFB,因为∠EGB=∠HGF,即可推出∠HGF=∠HFG解决问题.
(2)连接AF,作HK⊥FG于K.首先证明tan∠B=tan∠KHG=$\frac{KG}{HK}$=$\frac{1}{2}$,由tan∠B=$\frac{EG}{EB}$=$\frac{AF}{BF}$=$\frac{1}{2}$,设EG=a,则EB=2a,BG=$\sqrt{5}$a,BF=$\sqrt{5}$a+2$\sqrt{5}$,AF=$\frac{\sqrt{5}}{2}$a+$\sqrt{5}$,
在Rt△ABF中,根据AB2=AF2+BF2,列出方程102=($\frac{\sqrt{5}}{2}$a+$\sqrt{5}$)2+($\sqrt{5}$a+2$\sqrt{5}$)2,求出a=2,推出EG=2,BE=4,AE=6,在Rt△AEG中,根据AG=$\sqrt{A{E}^{2}+E{G}^{2}}$计算即可.
解答 (1)证明:如图,连接OF.
∵HF是切线,
∴OF⊥FH,
∴∠OFH=90°,
∴∠HFG+∠OFB=90°,
∵AB⊥CD,
∴∠BEG=90°,
∴∠OBF+∠EGB=90°,
∵OB=OF,
∴∠OBF=∠OFB,∵∠EGB=∠HGF,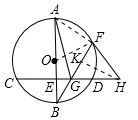
∴∠HGF=∠HFG,
∴FH=HG.
(2)解:连接AF,作HK⊥FG于K.
∵HF=HG,HK⊥FG,
∴FK=KG=$\sqrt{5}$,
∵AB=2FH=10,
∴HF=HG=5,
∴HK=$\sqrt{H{F}^{2}-F{K}^{2}}$=$\sqrt{{5}^{2}-(\sqrt{5})^{2}}$=2$\sqrt{5}$,
∵∠BEG=∠HKG=90°,∠BGE=∠HGK,
∴∠EBG=∠KHG,
∴tan∠B=tan∠KHG=$\frac{KG}{HK}$=$\frac{1}{2}$,
∵tan∠B=$\frac{EG}{EB}$=$\frac{AF}{BF}$=$\frac{1}{2}$,设EG=a,则EB=2a,BG=$\sqrt{5}$a,BF=$\sqrt{5}$a+2$\sqrt{5}$,AF=$\frac{\sqrt{5}}{2}$a+$\sqrt{5}$,
在Rt△ABF中,∵AB2=AF2+BF2,
∴102=($\frac{\sqrt{5}}{2}$a+$\sqrt{5}$)2+($\sqrt{5}$a+2$\sqrt{5}$)2,
∴a=2,
∴EG=2,BE=4,AE=6,
在Rt△AEG中,AG=$\sqrt{A{E}^{2}+E{G}^{2}}$=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$.
点评 本题考查切线的性质、等腰三角形的判定和性质、锐角三角函数、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形,学会用方程的首先思考问题,属于中考常考题型.

 互动英语系列答案
互动英语系列答案| A. | 2cm,3cm,4cm,5cm | B. | 1cm,$\sqrt{2}$cm,2cm,$\sqrt{2}$cm | ||
| C. | 1.5cm,2.5cm,4.5cm,6.5cm | D. | 1.1cm,2.2cm,3.3cm,4.4cm |
| A. | y=(x-2)2 | B. | y=(x+2)2 | C. | y=x2-2 | D. | y=x2+2 |
| A. | 矩形 | B. | 正方形 | C. | 菱形 | D. | 等腰梯形 |
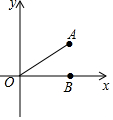 如图,在平面直角坐标系xOy中,已知点A(4,3)和点B(4,0),则sin∠AOB的值等于( )
如图,在平面直角坐标系xOy中,已知点A(4,3)和点B(4,0),则sin∠AOB的值等于( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |



