题目内容
6.已知,3<m<6,且点A(m,y1),B($\frac{1}{3}$m+1,y2),C(2,y3)都在二次函数y=$\sqrt{5}$x2-2$\sqrt{5}$x+3的图象上,则下列说法正确的是( )| A. | y2<y1<y3 | B. | y2<y3<y1 | C. | y3<y2<y1 | D. | y1<y3<y2 |
分析 根据m的范围,确定2、$\frac{1}{3}$m+1、m的大小,根据二次根式的性质求出平武县的对称轴,根据二次函数的性质解答.
解答 解:∵3<m<6,
∴2<$\frac{1}{3}$m+1<3,
∴2<$\frac{1}{3}$m+1<m,
y=$\sqrt{5}$x2-2$\sqrt{5}$x+3=$\sqrt{5}$(x-1)2+3-$\sqrt{5}$,
∵a=$\sqrt{5}$>0,
∴x>1时,y随x的最大而最大,
∴y3<y2<y1,
故选:C.
点评 本题考查的是二次函数图象上点的坐标特征,掌握二次函数的性质、灵活运用数形结合思想是解题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
16.计算-5x2+4x2的结果为( )
| A. | -1 | B. | x2 | C. | -9x2 | D. | -x2 |
17.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0,剩余部分沿虚线又剪开拼成一个长方形(不重叠无缝隙),则长方形的周长为( )cm.


| A. | 2a+5 | B. | 4a+10 | C. | 4a+16 | D. | 6a+15 |
14.将抛物线y=x2向右平移2个单位所得抛物线的函数表达式为( )
| A. | y=(x-2)2 | B. | y=(x+2)2 | C. | y=x2-2 | D. | y=x2+2 |
1.一个三角形的两边长分别是3cm和8cm,则此三角形的第三边的长可能是( )
| A. | 3cm | B. | 5cm | C. | 8cm | D. | 11cm |
11.顺次连结对角线互相垂直平分的四边形的各边中点,所组成的四边形是( )
| A. | 矩形 | B. | 正方形 | C. | 菱形 | D. | 等腰梯形 |




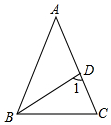 如图,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC,则∠1的度数是72°.
如图,在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC,则∠1的度数是72°.