题目内容
19. 如图,已知过原点的直线与双曲线$y=\frac{k}{x}$(k>0)交于A、B两点,点A到x轴的距离是它到y轴距离的一半,点B的纵坐标为-2.
如图,已知过原点的直线与双曲线$y=\frac{k}{x}$(k>0)交于A、B两点,点A到x轴的距离是它到y轴距离的一半,点B的纵坐标为-2.(1)求直线AB的解析式;
(2)求k的值;
(3)过原点O的另一条直线l交双曲线$y=\frac{k}{x}$(k>0)于P,Q两点(点P在第一象限),若以A,B,P,Q为顶点的四边形面积为24,求点P的坐标.
分析 (1)如图1,作辅助线,证明△AOC∽△BOD,根据OC=2AC,得OD=2BD,由此得出点B的坐标,利用待定系数法求直线AB的解析式;
(2)因为点B在反比例函数的图象上,所以把点B的坐标代入反比例函数解析式中可得k的值;
(3)根据中心对称的性质可得:四边形APBQ是平行四边形,得出△AOP的面积为6,设设P(m,$\frac{8}{m}$)(m>0,且m≠4),根据△AOP的面积列等式可求出m的值,从而得到点P的坐标.
解答 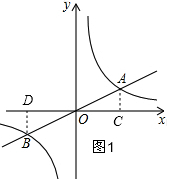 解:(1)如图1,过A作AC⊥x轴于C,过B作BD⊥x轴于D,则AC∥BD,
解:(1)如图1,过A作AC⊥x轴于C,过B作BD⊥x轴于D,则AC∥BD,
由题意得:OC=2AC,
∵AC∥BD,
∴△AOC∽△BOD,
∴$\frac{AC}{OC}=\frac{BD}{OD}$,
∴$\frac{BD}{OD}=\frac{AC}{2AC}$=$\frac{1}{2}$,
∴OD=2BD,
∵点B的纵坐标为-2,
∴BD=2,
∴OD=4,
∴B(-4,-2),
设直线AB的解析式为:y=kx,
把B(-4,-2)代入得:-4k=-2,
k=$\frac{1}{2}$,
∴直线AB的解析式为:y=2x;
(2)把B(-4,-2)代入y=$\frac{k}{x}$中得:k=-4×(-2)=8;
(3)如图2,∵反比例函数的图象是关于原点O的中心对称图形,
∴OP=OQ,OA=OB,
∴四边形APBQ是平行四边形,
∴S△POA=$\frac{1}{4}$S平行四边形APBQ=$\frac{1}{4}$×24=6,
设P(m,$\frac{8}{m}$)(m>0,且m≠4),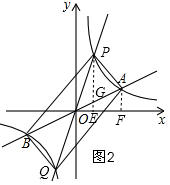
分别过P、A作x轴的垂线,垂足分别为E、F,则G(m,$\frac{m}{2}$),
∵B(-4,-2),
∴A(4,2),
∴OF=4,
PG=$\frac{8}{m}$-$\frac{m}{2}$,
∴S△POA=S△POG+S△PAG=$\frac{1}{2}$PG•OE+$\frac{1}{2}$PG•EF=$\frac{1}{2}$PG•OF,
∴$\frac{1}{2}$×4($\frac{8}{m}$-$\frac{m}{2}$)=6,
m2+6m-16=0,
(m+8)(m-2)=0,
m1=-8(舍),m2=2,
∴P(2,4).
点评 本题考查了反比例函数与一次函数的交点问题,考查了利用待定系数法求函数的解析式及中心对称的性质,掌握反比例函数是中心对称图形,同时将平行四边形的面积转化为三角形的面积求解.

| A. | 23和32 | B. | -33和(-3)3 | C. | -22和(-2)2 | D. | -($\frac{2}{3}$)3和-$\frac{{2}^{3}}{3}$ |
| A. | 若a是实数,则|a|≥0 | B. | 抛一枚硬币,正面朝上 | ||
| C. | 明天会下雨 | D. | 打开电视,正在播放新闻 |
| A. | y=(x-2)2 | B. | y=(x+2)2 | C. | y=x2-2 | D. | y=x2+2 |
| A. | 5或-5 | B. | 1或-1 | C. | 5或1 | D. | -5或-1 |
| A. | 矩形 | B. | 正方形 | C. | 菱形 | D. | 等腰梯形 |