题目内容
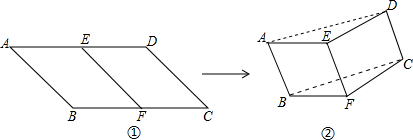
如果把平行四边形ABCD纸片沿EF折起，如图①，当折痕EF满足什么条件时，折起后由A，B，C，D四点组成的四边形仍是平行四边形（如图②）？并说明理由．
考点：平行四边形的判定与性质,翻折变换（折叠问题）
专题：
分析：利用平行四边形的性质与判定得出满足EF∥AB时仍是平行四边形．
解答：解：满足EF∥AB时仍是平行四边形，
理由：∵四边形ABCD是平行四边形，
∴AB
CD，AD
BC，
∵AB∥EF，AE∥BF，
∴四边形ABFE是平行四边形，
∴AB=EF=CD，
则AB
CD，
即由A，B，C，D四点组成的四边形仍是平行四边形．
理由：∵四边形ABCD是平行四边形，
∴AB
| ∥ |
. |
| ∥ |
. |
∵AB∥EF，AE∥BF，
∴四边形ABFE是平行四边形，
∴AB=EF=CD，
则AB
| ∥ |
. |
即由A，B，C，D四点组成的四边形仍是平行四边形．
点评：此题主要考查了平行四边形的性质判定与性质，正确把握平行四边形的性质是解题关键．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
如图，如果AB∥CD，AE平分∠BAC，CE平分∠ACD，试说明AE⊥CE．
如图，将边长为1的等边三角形ABC沿直线l向右翻动（不滑动）至如图位置，求点B从开始到结束所经过的路径与直线l所围成的图形面积．