题目内容
 如图,有一艘油轮在海上的A处遇险,立即向救援基地C发出通知.救援基地发现有一艘救援船在B处,距离A处最近,于是通知B处的救援船迅速赶往A处营救.已知C在A的东南方向,且BA=20 nmile,AC=99 nmile,BC=101 nmile,请确定救援船前进的方向.
如图,有一艘油轮在海上的A处遇险,立即向救援基地C发出通知.救援基地发现有一艘救援船在B处,距离A处最近,于是通知B处的救援船迅速赶往A处营救.已知C在A的东南方向,且BA=20 nmile,AC=99 nmile,BC=101 nmile,请确定救援船前进的方向.考点:解直角三角形的应用-方向角问题
专题:
分析:如图,作BG⊥x轴.根据勾股定理逆定理得到△ABC为直角三角形,可求出∠BAC=90°,再根据∠DAB=45°,判断出救援船前进方向.
解答: 解:如图,作BG⊥x轴.
解:如图,作BG⊥x轴.
∵BA=20 nmile,AC=99 nmile,BC=101 nmile,
∴BA2+AC2=202+992=10201nmile,BC2=1012=10201nmile,
∴BA2+AC2=BC2,
∴∠BAC=90°,
∵C在A的东南方向,
∴∠DAC=45°,
∴∠DAB=45°,
∴∠ABG=45°,
∴救援船前进的方向为东北方向.
 解:如图,作BG⊥x轴.
解:如图,作BG⊥x轴.∵BA=20 nmile,AC=99 nmile,BC=101 nmile,
∴BA2+AC2=202+992=10201nmile,BC2=1012=10201nmile,
∴BA2+AC2=BC2,
∴∠BAC=90°,
∵C在A的东南方向,
∴∠DAC=45°,
∴∠DAB=45°,
∴∠ABG=45°,
∴救援船前进的方向为东北方向.
点评:本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 如图,四边形ABCD中,AB=AD,∠BAD=90°,∠CBD=30°,∠BCD=45°,若AB=8
如图,四边形ABCD中,AB=AD,∠BAD=90°,∠CBD=30°,∠BCD=45°,若AB=8 如图,直线MN和直线DE分别是线段AB,BC的垂直平分线,它们交于P点,请问PA和PC相等吗?请说明理由.
如图,直线MN和直线DE分别是线段AB,BC的垂直平分线,它们交于P点,请问PA和PC相等吗?请说明理由.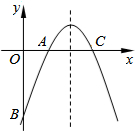 如图,已知二次函数y=-
如图,已知二次函数y=-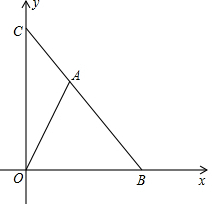 如图,已知点B的坐标为(4,0)点C的坐标为(0,4)点A在线段BC上,且不与点B,C重合.
如图,已知点B的坐标为(4,0)点C的坐标为(0,4)点A在线段BC上,且不与点B,C重合. 作图题:已知△ABC在平面直角坐标系中的位置如图所示,A(0,6),B(-2,-2),C(6,-5),求作:△ABC关于y轴的对称图形△A′B′C′.(保留作图痕迹)
作图题:已知△ABC在平面直角坐标系中的位置如图所示,A(0,6),B(-2,-2),C(6,-5),求作:△ABC关于y轴的对称图形△A′B′C′.(保留作图痕迹)