题目内容
7. 如图,在△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D,BE平分AC,则DE=$\frac{\sqrt{5}-2}{2}$.
如图,在△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D,BE平分AC,则DE=$\frac{\sqrt{5}-2}{2}$.
分析 根据题意和黄金三角形的概念得到点D是线段AC的黄金分割点,根据黄金比值求出AD,根据中点的性质求出AE,计算即可.
解答 解:∵∠A=36°,BD平分∠ABC交AC于点D,
∴点D是线段AC的黄金分割点,
∴AD=$\frac{\sqrt{5}-1}{2}$AB=$\frac{\sqrt{5}-1}{2}$,
∵BE平分AC,
∴AE=$\frac{1}{2}$AB=$\frac{1}{2}$,
∴DE=$\frac{\sqrt{5}-1}{2}$-$\frac{1}{2}$=$\frac{\sqrt{5}-2}{2}$,
故答案为:$\frac{\sqrt{5}-2}{2}$.
点评 本题考查的是黄金分割的概念以及黄金三角形的概念,掌握把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值$\frac{\sqrt{5}-1}{2}$叫做黄金比是解题的关键.

练习册系列答案
相关题目
15.一个几何体的三视图如图所示,则这个几何体可能是( )


| A. | 圆锥 | B. | 球 | C. | 圆柱 | D. | 圆 |
2. 画函数y=2x+1的图象(先填下表,再在图中的直角坐标系中描点,连线)
画函数y=2x+1的图象(先填下表,再在图中的直角坐标系中描点,连线)
 画函数y=2x+1的图象(先填下表,再在图中的直角坐标系中描点,连线)
画函数y=2x+1的图象(先填下表,再在图中的直角坐标系中描点,连线) | x | -2.5 | -2 | -1 | 0 | 1 | 2 | 2.5 |
| y |
 [背景知识]数轴是初中数学的一个重要工具,利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a-b|,若a>b,则可简化为AB=a-b;线段AB的中点M表示的数为$\frac{a+b}{2}$.
[背景知识]数轴是初中数学的一个重要工具,利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a-b|,若a>b,则可简化为AB=a-b;线段AB的中点M表示的数为$\frac{a+b}{2}$.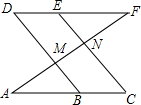 如图.已知∠D=∠C,∠AMB=∠ENF,求证:DF∥AC.
如图.已知∠D=∠C,∠AMB=∠ENF,求证:DF∥AC. 如图,矩形ACBE中,AC=6,BC=8,D是AB上一动点,当AD=$\frac{11}{5}$时,∠BDC=2∠BAE.
如图,矩形ACBE中,AC=6,BC=8,D是AB上一动点,当AD=$\frac{11}{5}$时,∠BDC=2∠BAE.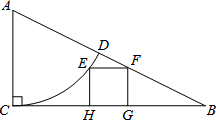 如图,Rt△ABC中,∠ACB=90°,AC=5,CB=10.以点A为圆心,AC长为半径的弧CD交AB于点D,点E是弧CD上任意一点,EH⊥BC于点H,以EH为边长作正方形EHGF,点F在AB边上,则S正方形EFGH=4.
如图,Rt△ABC中,∠ACB=90°,AC=5,CB=10.以点A为圆心,AC长为半径的弧CD交AB于点D,点E是弧CD上任意一点,EH⊥BC于点H,以EH为边长作正方形EHGF,点F在AB边上,则S正方形EFGH=4. 如图,C,F是线段BE上的两点,△ABF≌△DEC,且AC=DF.
如图,C,F是线段BE上的两点,△ABF≌△DEC,且AC=DF. 已知△ABC中,∠ABC=45°,AB=$\frac{5}{2}$$\sqrt{2}$,BC=12,将线段AC绕点A逆时针旋转90°,线段AD,连接BD,求BD的长.
已知△ABC中,∠ABC=45°,AB=$\frac{5}{2}$$\sqrt{2}$,BC=12,将线段AC绕点A逆时针旋转90°,线段AD,连接BD,求BD的长.