题目内容
2. 如图,在△ABC中,∠B=60°,∠BAC、∠ACB的平分线AE、CF相交于点O.求证:
如图,在△ABC中,∠B=60°,∠BAC、∠ACB的平分线AE、CF相交于点O.求证:(1)OE=OF;
(2)AF+CE=AC.
分析 (1)在AC上取AF=AM,连接OE,根据三角形的内角和定理,可得出∠BAC+∠BCA=120°,由角平分线的定义可得出∠OAC+∠OCA=60°,再根据外角的性质得出∠AOF的度数;根据SAS证明△AOF≌△AOM,得出OM=OF,再根据ASA证明△COE≌△COM,得出OM=OE,从而得出OF=OE.
(2)由△COE≌△COM,得到CM=CE,又AF=AM,所以得到AC=AM+CM=AF+CE.
解答 解:(1)如图,在AC上取AF=AM,连接OE,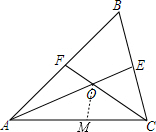
∵∠B=60°,
∴∠BAC+∠BCA=120°,
∵∠BAC、∠ACB的平分线AE、CF相交于点O,
∴∠BAC=2∠OAC,∠BCA=2∠OCA,
∴∠AOF=∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=60°;
∵∠BAC、∠ACB的平分线AE、CF相交于点O,
∴∠FAO=∠MAO,∠ECO=∠MCO,
在△FAO和△MAO中,
$\left\{\begin{array}{l}{AF=AM}\\{∠FAO=∠MAO}\\{AO=AO}\end{array}\right.$,
∴△FAO≌△MAO(SAS),
∴OM=OF,∠AOF=∠AOM=60°,
∴∠COE=∠COM=60°,
在△COE和△COM中,
$\left\{\begin{array}{l}{∠ECO=∠MCO}\\{OC=OC}\\{∠EOC=∠MOC}\end{array}\right.$,
∴△COE≌△COM(ASA),
∴OM=OE,
∴OE=OF.
(2)∵△COE≌△COM,
∴CM=CE,
∵AF=AM,
∴AC=AM+CM=AF+CE.
点评 本题考查了全等三角形的性质定理与判定定理,解决本题的关键是作出辅助线,证明三角形全等.

 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 画函数y=2x+1的图象(先填下表,再在图中的直角坐标系中描点,连线)
画函数y=2x+1的图象(先填下表,再在图中的直角坐标系中描点,连线) | x | -2.5 | -2 | -1 | 0 | 1 | 2 | 2.5 |
| y |
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
| A. | $\frac{4}{3}x$ | B. | $\frac{4}{3}xy$ | C. | $-\frac{4}{3}x$ | D. | $-\frac{4}{3}x{y^{10}}$ |
 如图,△ABC与△BDE为等边三角形,连接AD,EC,AD中点为M,EC中点为N,BM,BN,MN,求证:△BMN为等边三角形.
如图,△ABC与△BDE为等边三角形,连接AD,EC,AD中点为M,EC中点为N,BM,BN,MN,求证:△BMN为等边三角形. 已知△ABC中,∠BAC=90°,四边形ABDE、BCFG是两个正方形,AB的延长线交DG于P,求证:AC=2BP.
已知△ABC中,∠BAC=90°,四边形ABDE、BCFG是两个正方形,AB的延长线交DG于P,求证:AC=2BP. 如图,已知△ABC中,F是高AD和BE的交点,AD=BD,CD=4,AF=3,求DA的长.
如图,已知△ABC中,F是高AD和BE的交点,AD=BD,CD=4,AF=3,求DA的长. 已知△ABC中,∠ABC=45°,AB=$\frac{5}{2}$$\sqrt{2}$,BC=12,将线段AC绕点A逆时针旋转90°,线段AD,连接BD,求BD的长.
已知△ABC中,∠ABC=45°,AB=$\frac{5}{2}$$\sqrt{2}$,BC=12,将线段AC绕点A逆时针旋转90°,线段AD,连接BD,求BD的长.