Question

15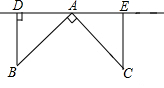．如图，点A、D、E在直线l上，∠BAC=90°，AB=AC，BD⊥l于D，CE⊥l于E，求证：DE=BD+CE．

Answer 1

分析 根据已知条件及互余关系可证△ABD≌△CAE，则BD=AE，AD=CE，由DE=AD+AE，得出线段DE=BD+CE．

解答 证明：∵∠BAC=90°，BD⊥DE，CE⊥DE，
∴∠DAB+∠DBA=∠DAB+∠EAC，
∴∠DBA=∠EAC；
在△ABD与△CAE中，
$\left\{\begin{array}{l}{∠DBA=∠EAC}\\{∠BDA=∠AEC}\\{AB=AC}\end{array}\right.$，
∴△ABD≌△CAE（AAS），
∴BD=AE，AD=CE，
∴DE=BD+CE．

点评 该题主要考查了全等三角形的判定及其性质的应用问题；准确找出命题中隐含的等量关系，是证明全等三角形的关键．