题目内容
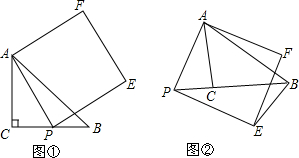
10.已知△ACB为等腰直角三角形,点P在BC上,以AP为边长作正方形APEF.(1)如图①,当点P在BC上时,求∠EBP;
(2)如图②,当点P在BC的延长线上时,求∠EBP.
分析 (1)过E作CB垂线,交延长线于点M,可证△ACP≌△PEM,得出EM=PC,AC=PM,得出BM=EM,得出∠EBM=45°,求得∠EBP;
(2)类比(1)的方法同样过E作CB垂线,垂足M,最后得出BM=EM,得出∠EBM=45°得出结论.
解答 解:(1)如图,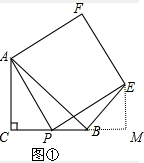
过E作CB垂线,交延长线于点M,
∵四边形APEF是正方形,
∴∠APE=90°,AP=PE,
∵∠APC+∠PAC=∠APC+∠EPM=90°,
∴∠PAC=∠EPM,
在△ACP和△PEM中,
$\left\{\begin{array}{l}{∠PAC=∠EPM}\\{∠C=∠M}\\{AP=PE}\end{array}\right.$,
∴△ACP≌△PEM,
∴AC=MP,PC=EM,
∵AC=BC,
∴BC=MP,
∴PC=BM,
∴BM=EM,
∴∠EBM=45°,
∴∠EBP=135°.
(2)如图,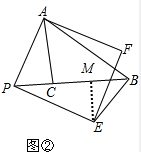
作EM⊥CB,垂足为M,
∵四边形APEF是正方形,
∴∠APE=90°,AP=PE,
∵∠APC+∠PAC=∠APC+∠EPM=90°,
∴∠PAC=∠EPM,
在△ACP和△PEM中,
$\left\{\begin{array}{l}{∠PAC=∠EPM}\\{∠C=∠M}\\{AP=PE}\end{array}\right.$,
∴△ACP≌△PEM,
∴AC=MP,PC=EM,
∵AC=BC,
∴BC=MP,
∴PC=BM,
∴BM=EM,
∴∠EBM=45°.
点评 此题考查三角形全等的判定与性质,等腰直角三角形的性质,正确作出辅助线,利用三角形全等的证明方法得出三角形全等是解决问题的关键.

练习册系列答案
相关题目
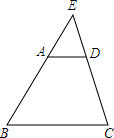 如图,在梯形ABCD中,AD∥BC,延长两腰交于点E,若AD=2,BC=6,AB=4,则$\frac{ED}{EC}$=$\frac{1}{3}$,$\frac{DE}{DC}$=$\frac{1}{2}$.
如图,在梯形ABCD中,AD∥BC,延长两腰交于点E,若AD=2,BC=6,AB=4,则$\frac{ED}{EC}$=$\frac{1}{3}$,$\frac{DE}{DC}$=$\frac{1}{2}$. 如图,向△ABC外作正方形ABEF和ACGH,点M是BC边的中点,求证:FH=2AM.
如图,向△ABC外作正方形ABEF和ACGH,点M是BC边的中点,求证:FH=2AM.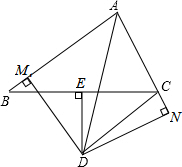 如图,在△ABC中,AD平分∠BAC,DE所在直线是BC的垂直平分线,E为垂足,过点D作DM⊥AB于点M,DN⊥AC交AC的延长线于点N.求证:
如图,在△ABC中,AD平分∠BAC,DE所在直线是BC的垂直平分线,E为垂足,过点D作DM⊥AB于点M,DN⊥AC交AC的延长线于点N.求证:
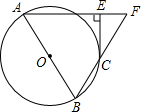 如图,AB为⊙O的直径,AE⊥CE于点E,BC的延长线与AE的延长线相交于点F.若CE为⊙O的切线,AF=BF,求∠A的度数.
如图,AB为⊙O的直径,AE⊥CE于点E,BC的延长线与AE的延长线相交于点F.若CE为⊙O的切线,AF=BF,求∠A的度数.
 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC与点E,PF⊥CD于点F,连接EF,给出的下列结论:①AP=EF;②∠PFE=∠BAP;③PD=EC;④PB2+PD2=2PA2,正确的个数有( )
如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC与点E,PF⊥CD于点F,连接EF,给出的下列结论:①AP=EF;②∠PFE=∠BAP;③PD=EC;④PB2+PD2=2PA2,正确的个数有( )