题目内容
12.已知关于x的方程x2-6x+3m-2=0(1)若方程有两个正根,求m的取值范围;
(2)若方程的两个根都大于1,求m的取值范围;
(3)若方程的两个根一个大于1,一个小于1,求m的取值范围.
分析 (1)根据根与系数的关系得到x1x2<0,此时方程一定有实数解,然后解不等式即可;
(2)若方程的两个根都大于1,即(x1-1)和(x2-1)同号,且和大于0,根据根与系数的关系列不等式解得;
(3)方程的两个根一个大于1,一个小于1,即x1-1和x2-1异号,利用根与系数的关系列不等式求解.
解答 解:∵x2-6x+3m-2=0,
∴△=36-4(3m-2)=44-12m,
∴x1+x2=6,x1x2=3m-2.
(1)根据题意得:$\left\{\begin{array}{l}{44-12m>0}\\{3m-2>0}\end{array}\right.$,
解得:$\frac{2}{3}$<m<$\frac{11}{3}$;
(2)根据题意得:$\left\{\begin{array}{l}{44-12m>0}\\{{1}^{2}-6×1+3m-2>0}\end{array}\right.$,
解得:$\frac{7}{3}$<m<$\frac{11}{3}$;
(3)根据题意得:$\left\{\begin{array}{l}{44-12m>0}\\{({x}_{1}-1)({x}_{2}-1)=3m-7<0}\end{array}\right.$,
解得:m<$\frac{7}{3}$.
点评 本题考查的知识点是一元二次方程根与系数的关系以及根的判别式等知识,其中由韦达定理(一元二次方程根与系数的关系)结合已知,构造出关k的不等式组是解答本题的关键.

练习册系列答案
相关题目
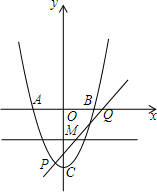 如图,抛物线y=x2-4分别交x轴于A、B,交y轴于C,P为第三象限的抛物线上一点,过P点的直线y=kx-3交直线y=-2于点M,交抛物线于另一点Q,若P、Q两点关于M成中心对称,求k的值.
如图,抛物线y=x2-4分别交x轴于A、B,交y轴于C,P为第三象限的抛物线上一点,过P点的直线y=kx-3交直线y=-2于点M,交抛物线于另一点Q,若P、Q两点关于M成中心对称,求k的值.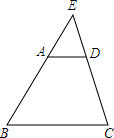 如图,在梯形ABCD中,AD∥BC,延长两腰交于点E,若AD=2,BC=6,AB=4,则$\frac{ED}{EC}$=$\frac{1}{3}$,$\frac{DE}{DC}$=$\frac{1}{2}$.
如图,在梯形ABCD中,AD∥BC,延长两腰交于点E,若AD=2,BC=6,AB=4,则$\frac{ED}{EC}$=$\frac{1}{3}$,$\frac{DE}{DC}$=$\frac{1}{2}$.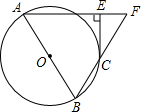 如图,AB为⊙O的直径,AE⊥CE于点E,BC的延长线与AE的延长线相交于点F.若CE为⊙O的切线,AF=BF,求∠A的度数.
如图,AB为⊙O的直径,AE⊥CE于点E,BC的延长线与AE的延长线相交于点F.若CE为⊙O的切线,AF=BF,求∠A的度数.