题目内容
17.把y=-$\frac{1}{2}$x2的图象向上平移2个单位.(1)求新图象的函数表达式、顶点坐标和对称轴;
(2)列函数对应值表,并作函数图象;
(3)求函数的最大值或最小值,并求此时x的值.
分析 (1)根据平移规律“上加下减”写出平移后的抛物线解析式;
(2)根据抛物线解析式列函数对应值表,并作函数图象;
(3)结合函数图象回答问题.
解答 解:(1)把y=-$\frac{1}{2}$x2的图象向上平移2个单位后得到抛物线的解析式为:y=-$\frac{1}{2}$x2+2,
所以它的顶点坐标是(0,2),对称轴是x=0.即y轴;
(2)由y=-$\frac{1}{2}$x2+2,得
| x | -6 | -4 | -2 | 0 | 2 | 4 | 6 | 8 |
| y | -16 | -6 | 0 | 2 | 0 | -6 | -16 | -30 |
 ;
;(3)如图所示:当x=0时,y最大=2.
点评 本题考查了二次函数图象与几何变换.要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
7.二次函数y=-3x2-6x+5的图象的顶点坐标是( )
| A. | (-1,2) | B. | (1,-4) | C. | (-1,8) | D. | (1,8) |
 已知:反比例函数y=$\frac{2}{x}$与一次函数交于点A,D,一次函数与x轴、y轴分别交于点C,B,求证:AB=CD.
已知:反比例函数y=$\frac{2}{x}$与一次函数交于点A,D,一次函数与x轴、y轴分别交于点C,B,求证:AB=CD.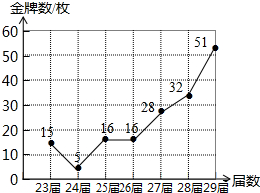 从1984年起,我国先后参加了第23届夏季奥运会,取得了骄人的成绩.如图是根据第23届至29届夏季奥运会我国获得的金牌数绘制的折线统计图,观察统计图可得:与上一届相比增长量最大的是第29届夏季奥运会,比它的上一届增加了19枚金牌.
从1984年起,我国先后参加了第23届夏季奥运会,取得了骄人的成绩.如图是根据第23届至29届夏季奥运会我国获得的金牌数绘制的折线统计图,观察统计图可得:与上一届相比增长量最大的是第29届夏季奥运会,比它的上一届增加了19枚金牌.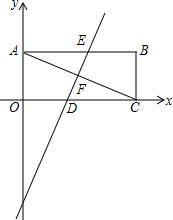 如图,平面直角坐标系中,矩形OABC的两条邻边分别在x轴、y轴上,对角线AC=4$\sqrt{5}$,边OA=4.
如图,平面直角坐标系中,矩形OABC的两条邻边分别在x轴、y轴上,对角线AC=4$\sqrt{5}$,边OA=4.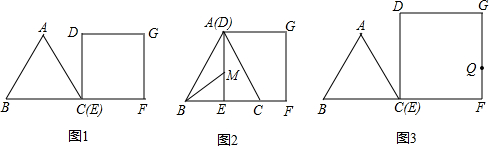
 已知BC为半圆O的直径,AD⊥BC,垂足为D,过点B作弦BF交AD于E,交半圆O于点F,弦AC与BF交于点H,且AE=BE,
已知BC为半圆O的直径,AD⊥BC,垂足为D,过点B作弦BF交AD于E,交半圆O于点F,弦AC与BF交于点H,且AE=BE,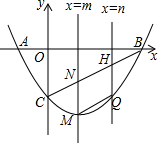 如图,在平面直角坐标系中,抛物线y=x2-2x-3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线x=m(m>0),直线x=n(n>0)(m<n)分别交线段BC于N点、H点,交抛物线于M点、Q点.当NH∥MQ时,求m+n的值.
如图,在平面直角坐标系中,抛物线y=x2-2x-3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线x=m(m>0),直线x=n(n>0)(m<n)分别交线段BC于N点、H点,交抛物线于M点、Q点.当NH∥MQ时,求m+n的值.