题目内容
5.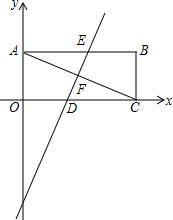 如图,平面直角坐标系中,矩形OABC的两条邻边分别在x轴、y轴上,对角线AC=4$\sqrt{5}$,边OA=4.
如图,平面直角坐标系中,矩形OABC的两条邻边分别在x轴、y轴上,对角线AC=4$\sqrt{5}$,边OA=4.(1)求C点的坐标;
(2)把矩形OABC沿直线DE对折使点C落在点A处,直线DE与OC、AC、AB的交点分别为D,F,E,求直线DE的函数关系式;
(3)若点M是y轴上一点,点N是坐标平面内一点,问能否找到合适的点M和点N使以点M、A、D、N为顶点的四边形是菱形?如果能找到,请直接写出点M的坐标;如果找不到,请说明原因.
分析 (1)由四边形AOCB为矩形,得到∠AOC为直角,在直角三角形AOC中,利用勾股定理求出OC的长,即可确定出C的坐标;
(2)根据矩形OABC沿直线DE对折使点C落在点A处,所以DE、AC互相垂直平分,得到AD=CD=AE=CE,设OD=x,则AD=CD=8-x,利用勾股定理在Rt△AOD中:AD2=OA2+OD2,即(8-x)2=x2+16,解得:x=3,从而确定D(3,0),E(5,4),利用待定系数法求直线DE的解析式,即可解答;
(3)设M(0,m),根据勾股定理可得AD=$\sqrt{0{A}^{2}+O{C}^{2}}=\sqrt{{4}^{2}+{3}^{2}}$=5,分两种情况考虑:①当AD是菱形的一条边是,②当AD是菱形的对角线时,求出点M的坐标即可.
解答 解:(1)∵AC=4$\sqrt{5}$,边OA=4.
∴OC=$\sqrt{A{C}^{2}-O{A}^{2}}=\sqrt{(4\sqrt{5})^{2}-{4}^{2}}$=8,
∴C(8,0).
(2)如图1所示,连接AD,CE,
∵矩形OABC沿直线DE对折使点C落在点A处,
∴DE、AC互相垂直平分,
∴AD=CD=AE=CE,
设OD=x,则AD=CD=8-x,
在Rt△AOD中:AD2=OA2+OD2,
即(8-x)2=x2+16,
解得:x=3,
∴OD=3,CD=AE=5,
∴D(3,0),E(5,4),
设直线DE的解析式为y=kx+b,
将D、E坐标代入得:$\left\{\begin{array}{l}{3k+b=0}\\{5k+b=4}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=2}\\{b=-6}\end{array}\right.$,
∴直线DE的解析式为y=2x-6.
(3)如图2所示,
设M(0,m)
∵OA=4,OD=3,
∴AD=$\sqrt{0{A}^{2}+O{C}^{2}}=\sqrt{{4}^{2}+{3}^{2}}$=5,
①当AD是菱形的一条边是,AN=AD,
即|4-m|=5,
解得:m1=9,m2=-1,
∴M1(0,9),M2(0,-1).
②当AD是菱形的对角线时,AM=DM,
即(4-m)2=m2+32,
解得:m=$\frac{7}{8}$,
∴M3(0,$\frac{7}{8}$).
点评 此题属于一次函数综合题,涉及的知识有:折叠的性质,坐标与图形性质,勾股定理,矩形的性质,菱形的性质,利用了分类讨论的思想,熟练掌握性质是解本题的关键.

 一个残破的车轮如图所示,测得它所剩圆弧两端点间的距离a=60cm,弧的中点到弧所对的弦的距离h=10cm,如果需要加工与原来大小相同的车轮,那么这个车轮的半径是多少?
一个残破的车轮如图所示,测得它所剩圆弧两端点间的距离a=60cm,弧的中点到弧所对的弦的距离h=10cm,如果需要加工与原来大小相同的车轮,那么这个车轮的半径是多少?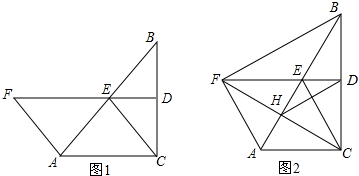
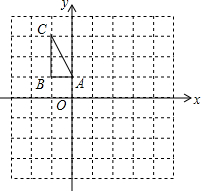 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3).
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3).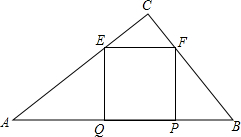 如图,在直角△ABC中,∠ACB=90°,若AC=40,BC=30,正方形EFPQ的一边QP在斜边AB上,C,F分别在AC、BC上,则该正方形的面积为$\frac{360000}{1369}$.
如图,在直角△ABC中,∠ACB=90°,若AC=40,BC=30,正方形EFPQ的一边QP在斜边AB上,C,F分别在AC、BC上,则该正方形的面积为$\frac{360000}{1369}$.