题目内容
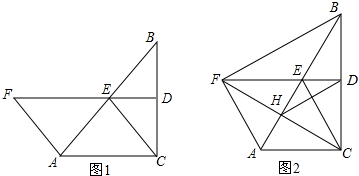
2. 已知BC为半圆O的直径,AD⊥BC,垂足为D,过点B作弦BF交AD于E,交半圆O于点F,弦AC与BF交于点H,且AE=BE,
已知BC为半圆O的直径,AD⊥BC,垂足为D,过点B作弦BF交AD于E,交半圆O于点F,弦AC与BF交于点H,且AE=BE,求证:(1)弧AB=弧AF;
(2)AH•BC=2AF•BE.
分析 (1)等腰△ABE中,∠BAD=∠ABE;由同角的余角相等知,∠BAD=∠C,故有∠C=∠ABF.由圆周角定理知,$\widehat{AB}$=$\widehat{AF}$;
(2)由于∠EAH=∠AHB,可得出AE=EH=BE=$\frac{1}{2}$BH,易证得Rt△ABH∽Rt△ACB.则AH:AB=BH:BC,即AH•BC=2AB•BE,由于AB=AF,于是得到结论.
解答 证明:(1)∵AE=BE,
∴∠BAD=∠ABE,
∵BC是直径,AD⊥BC,
∴∠ADB=∠BAC=90°,
∴∠ABD+∠BAD=∠ABC+∠C=90°,
∴∠BAD=∠C,
∴∠C=∠ABF,
∴$\widehat{AB}$=$\widehat{AF}$;
(2)∵∠C=∠ABF,
Rt△ABH∽Rt△ACB,
∴AH:BH=AB:BC,即AH•BC=AB•BH,
∵∠EAH+∠BAD=∠AHB+∠ABH=90°,∠BAD=∠ABE,
∴∠EAH=∠AHB,
∴AE=EH=BE=$\frac{1}{2}$BH,
∴AH•BC=2AB•BE,
由(1)证得$\widehat{AB}$=$\widehat{AF}$,
∴AB=AF,
∴AH•BC=2AF•BE.
点评 本题考查了等腰三角形的性质、圆周角定理、相似三角形的判定和性质,熟练掌握各定理是解题的关键.

练习册系列答案
相关题目
7.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
下列结论中正确的有4个.
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小;
(3)x=2是方程ax2+(b-1)x+c=0的一个根;
(4)当-1<x<2时,ax2+(b-1)x+c>0.
| x | -1 | 0 | 0.5 | 2 |
| y | -1 | 2 | 3.75 | 2 |
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小;
(3)x=2是方程ax2+(b-1)x+c=0的一个根;
(4)当-1<x<2时,ax2+(b-1)x+c>0.
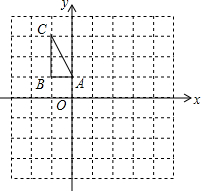 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3).
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3).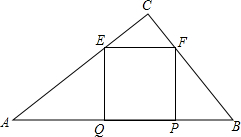 如图,在直角△ABC中,∠ACB=90°,若AC=40,BC=30,正方形EFPQ的一边QP在斜边AB上,C,F分别在AC、BC上,则该正方形的面积为$\frac{360000}{1369}$.
如图,在直角△ABC中,∠ACB=90°,若AC=40,BC=30,正方形EFPQ的一边QP在斜边AB上,C,F分别在AC、BC上,则该正方形的面积为$\frac{360000}{1369}$.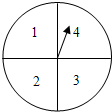 如图,把一个转盘分成四等份,依次标上数字:1,2,3,4,若连续自由转动转盘二次,指针指向的数字分别记作a,b,把a,b作为点A的横、纵坐标.
如图,把一个转盘分成四等份,依次标上数字:1,2,3,4,若连续自由转动转盘二次,指针指向的数字分别记作a,b,把a,b作为点A的横、纵坐标.