题目内容
1.已知点A(2,4),B(-2,-2),C(1,a)在一条直线上,则a=$\frac{5}{2}$.分析 先用待定系数法求出直线AB的解析式,再把C(1,a)代入求出出a的值即可.
解答 解:设直线AB的解析式为y=kx+b(k≠0),
∵A(2,4),B(-2,-2),
∴$\left\{\begin{array}{l}2k+b=4\\-2k+b=-2\end{array}\right.$,解得$\left\{\begin{array}{l}k=\frac{3}{2}\\ b=1\end{array}\right.$,
∴直线AB的解析式为y=$\frac{3}{2}$x+1,
∵C(1,a)在此直线上,
∴a=$\frac{3}{2}$+1=$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
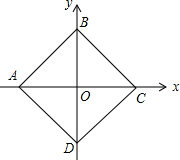 如图,在平面直角坐标系中,四边形ABCD是正方形,AB=$\sqrt{2}$,则点A的坐标为(-1,0)、点B的坐标为(0,1)、点C的坐标为(1,0)、点D的坐标为(0,-1).
如图,在平面直角坐标系中,四边形ABCD是正方形,AB=$\sqrt{2}$,则点A的坐标为(-1,0)、点B的坐标为(0,1)、点C的坐标为(1,0)、点D的坐标为(0,-1).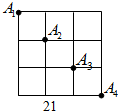 如图,点A1、A2、A3、A4是某市正方形道路网的部分交汇点,且它们都位于同一对角线上.某人从点A1出发,规定向右或向下行走,那么到达点A3的走法共有6种.
如图,点A1、A2、A3、A4是某市正方形道路网的部分交汇点,且它们都位于同一对角线上.某人从点A1出发,规定向右或向下行走,那么到达点A3的走法共有6种.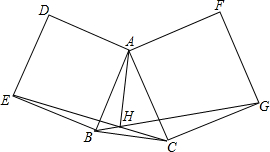 在△ABC的边AB,AC向外作正方形ABED,ACGF,BG、CE相交于H.求证:AH⊥BC.
在△ABC的边AB,AC向外作正方形ABED,ACGF,BG、CE相交于H.求证:AH⊥BC. 如图,点P是平行四边形ABCD对角线BD上的动点,点M为AD的中点,已知AD=8,AB=10,∠ABD=45°,把平行四边形ABCD绕着点A按逆时针方向旋转,点P的对应点是点Q,则线段MQ的长度的最大值与最小值的差为18-5$\sqrt{2}$.
如图,点P是平行四边形ABCD对角线BD上的动点,点M为AD的中点,已知AD=8,AB=10,∠ABD=45°,把平行四边形ABCD绕着点A按逆时针方向旋转,点P的对应点是点Q,则线段MQ的长度的最大值与最小值的差为18-5$\sqrt{2}$.