题目内容
19. 如图,点P是平行四边形ABCD对角线BD上的动点,点M为AD的中点,已知AD=8,AB=10,∠ABD=45°,把平行四边形ABCD绕着点A按逆时针方向旋转,点P的对应点是点Q,则线段MQ的长度的最大值与最小值的差为18-5$\sqrt{2}$.
如图,点P是平行四边形ABCD对角线BD上的动点,点M为AD的中点,已知AD=8,AB=10,∠ABD=45°,把平行四边形ABCD绕着点A按逆时针方向旋转,点P的对应点是点Q,则线段MQ的长度的最大值与最小值的差为18-5$\sqrt{2}$.
分析 如作AP1⊥BD垂足为P1,当AP1旋转到与射线AD的重合时(点P1与点E重合),ME就是MQ最小值,当点P2与B重合时,旋转到与DA的延长线重合时(点P2与点F重合),此时MF就是MQ最大值,分别求出MQ的最大值与最小值即可解决问题.
解答 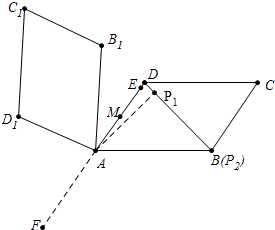 解:如图,作AP1⊥BD垂足为P1,
解:如图,作AP1⊥BD垂足为P1,
∵∠DBA=45°,AB=10,
∴∠P1AB=∠DBA=45°,AP1=P1B=5$\sqrt{2}$,
∵AM=MD=$\frac{1}{2}$AD=4,
当AP1旋转到与射线AD的重合时(点P1与点E重合),ME就是MQ最小值=5$\sqrt{2}$-4,
当点P2与B重合时,旋转到与DA的延长线重合时(点P2与点F重合),此时MF就是MQ最大值=AM+AF=14,
∴MQ的最大值与最小值的差=14-(5$\sqrt{2}$-4)=18-5$\sqrt{2}$.
故答案为18-5$\sqrt{2}$.
点评 本题考查旋转的性质、平行四边形的性质等知识,根据题意找到MQ最大值与最小值的位置是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.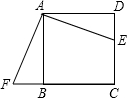 如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
 如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )| A. | 4 | B. | 8 | C. | 16 | D. | 无法计算 |
8. 如图,把一张长方形纸片ABCD沿EF折叠,若∠EFG=50°,则∠BGE=( )
如图,把一张长方形纸片ABCD沿EF折叠,若∠EFG=50°,则∠BGE=( )
 如图,把一张长方形纸片ABCD沿EF折叠,若∠EFG=50°,则∠BGE=( )
如图,把一张长方形纸片ABCD沿EF折叠,若∠EFG=50°,则∠BGE=( )| A. | 100° | B. | 90° | C. | 80° | D. | 70° |
 如图,AB=16cm,点D为射线AC上一点,且AD=20cm,点E是平面上任一点,且BE=3AE.
如图,AB=16cm,点D为射线AC上一点,且AD=20cm,点E是平面上任一点,且BE=3AE.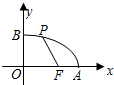 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,点F是x轴上一点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:①OA=5;②AF=1;③BF=5;④OB=3.其中正确结论的序号是①③.
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,点F是x轴上一点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:①OA=5;②AF=1;③BF=5;④OB=3.其中正确结论的序号是①③. 如图,点D、E分别是等边三角形ABC的两边AB、AC上的点,且∠BOD=60°,求证:AD=CE.
如图,点D、E分别是等边三角形ABC的两边AB、AC上的点,且∠BOD=60°,求证:AD=CE. 已知一次函数y=-$\frac{1}{2}$x+2和y=2x-3的图象分别交y轴与A、B两点,两个一次函数的图象相交于点P.
已知一次函数y=-$\frac{1}{2}$x+2和y=2x-3的图象分别交y轴与A、B两点,两个一次函数的图象相交于点P.